Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE-3|5 VideosSYSTEM OF A PARTICLES & ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE-4|7 VideosSYSTEM OF A PARTICLES & ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE-1|4 VideosSIMPLE HARMONIC MOTION
VMC MODULES ENGLISH|Exercise 7-previous year question|46 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise IMPECCABLE|56 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-SYSTEM OF A PARTICLES & ROTATIONAL MOTION-PRACTICE EXERCISE-2
- A wheel is at rest. Its angular velocity increases uniformly and becom...
Text Solution
|
- A wheel initially at rest, is rotated with a uniform angular accelerat...
Text Solution
|
- As a part of a maintenance inspection the compressor of a jet engine i...
Text Solution
|
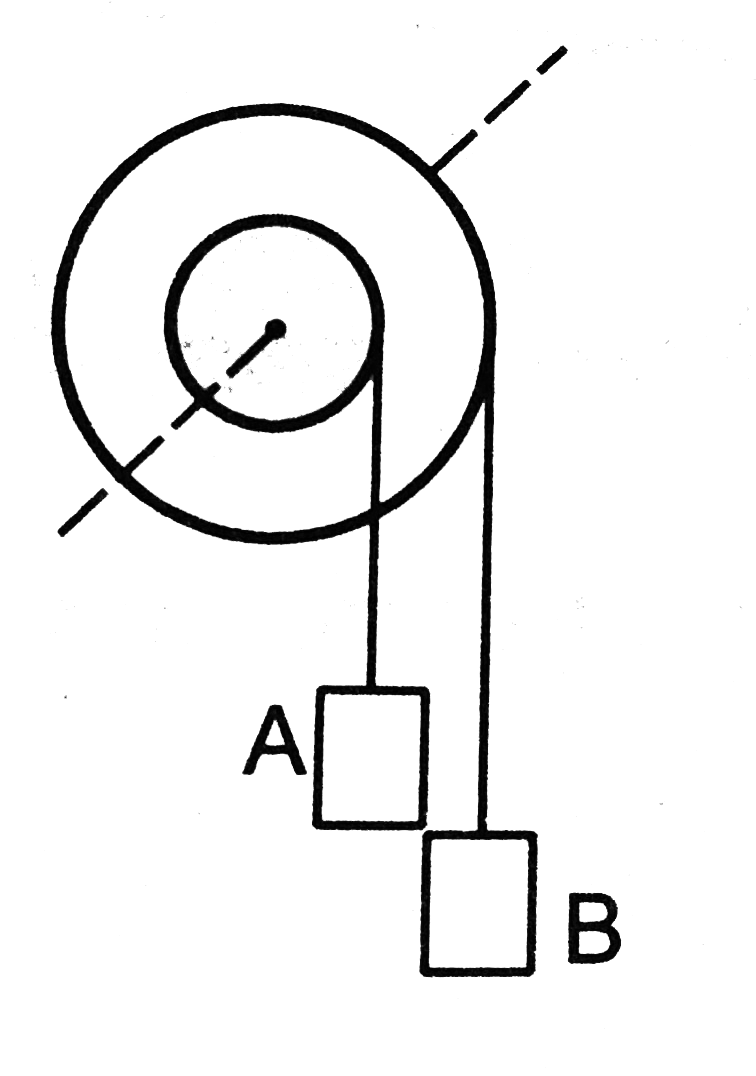
- Figure shows a small wheel fixed coaxially on a bigger one of double t...
Text Solution
|
- If the position vector of a particle is vecr=(3hati+4hatj) meter and I...
Text Solution
|