A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-MOCK TEST 3-PART I : PHYSICS (SECTION-2)
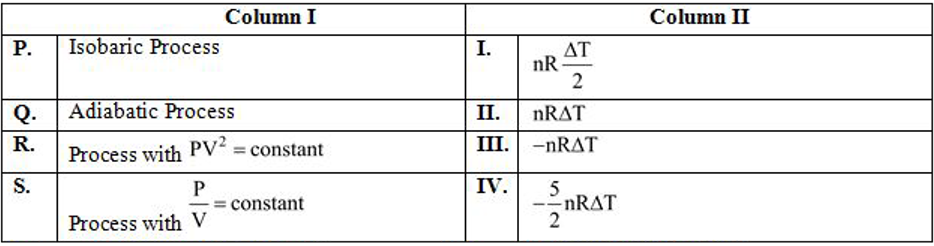
- Choose the option showing the correct match for work done by n moles o...
Text Solution
|
- A stationary vessel contains a mixture of equal moles of Nitrogen and ...
Text Solution
|
- A compound micrscope consists of an objective lens of focal length 1....
Text Solution
|
- ABC is a plane lamina of the shape of an equilateral triangle. D, E ar...
Text Solution
|
- Photons of energy 7eV fall on the surface of a metal X resulting in em...
Text Solution
|
- Two men each of mass m stand on the rim of a horizontal circular disc,...
Text Solution
|
- Three, 10W, 20V, 1000 mA Zener diodes are connected as shown in figure...
Text Solution
|
- An alternating voltage given by V=300sqrt2sin (50t) (in volts) is conn...
Text Solution
|
- There are two radioactive nuclei A and B A is an alpha emitter and B a...
Text Solution
|
- Unpolarized light passes through two polaroids, the axis of one is ver...
Text Solution
|
- The human eye has an approximate angluar resolution of phi=5.8xx10^(-4...
Text Solution
|