Home
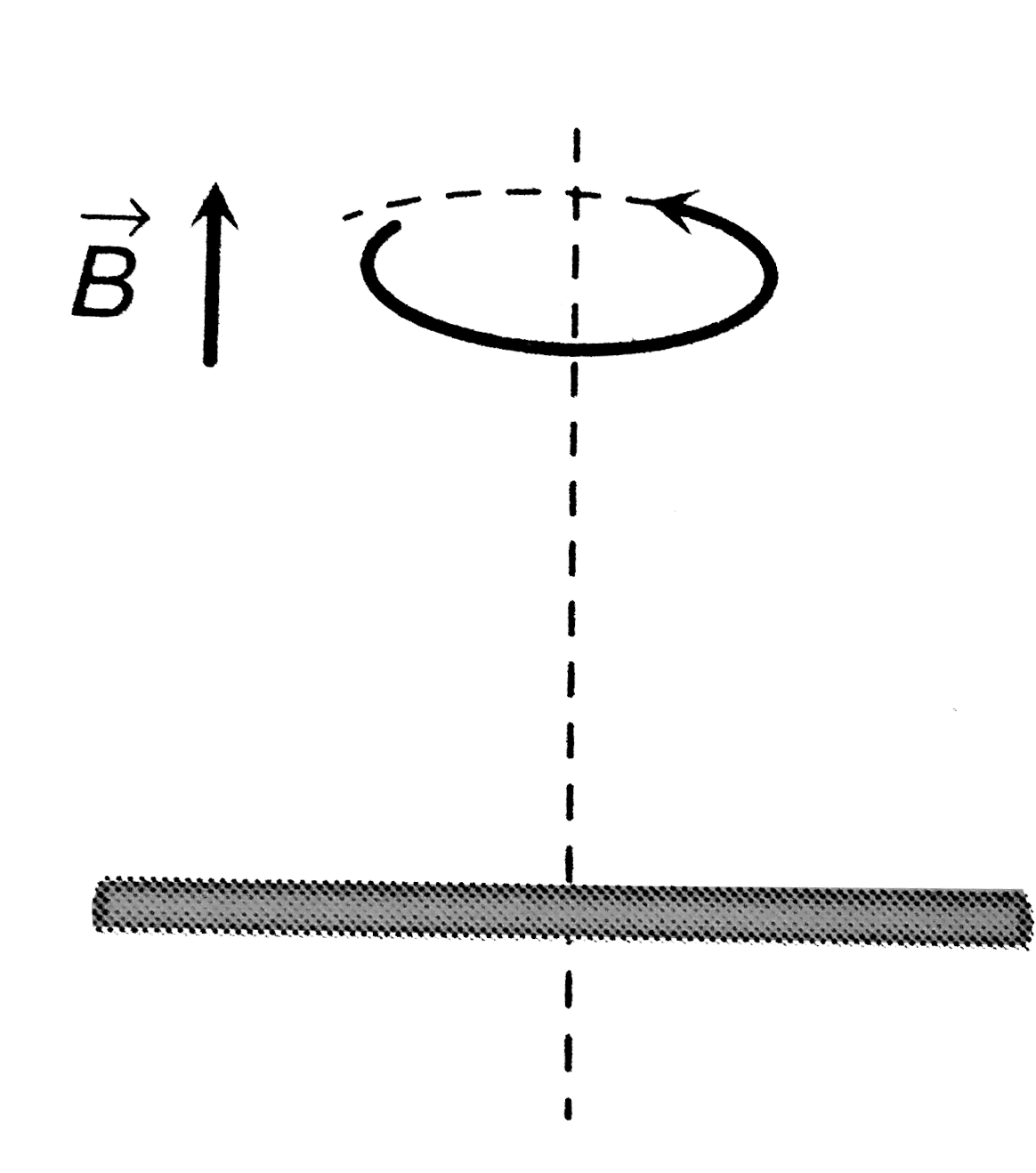
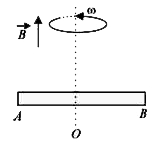
Class 12
PHYSICS
A conducting rod of length 2l is rotatin...

A conducting rod of length `2l` is rotating with constant angular speed `w` about its perpendicular bisector. A uniform magnetic field `B` exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

A

`B omega l^(2)`

B

`(1)/(2) B omegal^(2) `

C

`(1)/(8) omega l^(2) `

D

zero

Text Solution

Verified by Experts

The correct Answer is:
D
Potential difference between
`O and A ` is `V_A - V_O = (1)/(2) B l^(2) omega `
`O and B ` is `V_B - V_O = (1)/(2) B l^(2) omega `
So ` V_A - V_B = 0`
Promotional Banner

Topper's Solved these Questions

  • MOCK TEST 4

    VMC MODULES ENGLISH|Exercise PHYSICS (SECTION 2)|5 Videos

  • MOCK TEST 3

    VMC MODULES ENGLISH|Exercise PART I : PHYSICS (SECTION-2)|10 Videos

  • MOCK TEST 5

    VMC MODULES ENGLISH|Exercise PHYSICS ( SECTION-2)|5 Videos

Similar Questions

Explore conceptually related problems

A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is

A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is

A rod of length l rotates with a small but uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is

A conducting disc of radius r rotaes with a small but constant angular velocity omega about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.

A conducting rod OA of length l is rotated about its end O with an angular velocity omega in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.

A conducting rod of length l is rotating with constant angular velocity omega about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

A metal rod length l rotates about on end with a uniform angular velocity omega . A uniform magnetic field vecB exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they moving in circular paths.

A straight rod of length L is rotating about an axis passing through O and perpendicular to the plane. In the space a uniform magnetic field B exits normal to the plane of rotation. Potential difference between a & b is equal to

A conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T . Find the emf induced between the ends of the stick.

A conducting rod AB of length l is rotated about point O with an angular velocity velocity omega in a uniform magnetic field (B_0) directed perpendicular into the plane of rotation as shown in the figure. The value of V_B - V_A is