Home
Class 12
PHYSICS
A horizontal force F is applied at the t...

A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is `mu `,find `100 mu ? ( sqrt(3) = 1.74)`

Text Solution

Verified by Experts

The correct Answer is:
58
For toppling
`F.(a sqrt(3))/(2) =mg ,(a)/(2) , " " F=(mg)/(sqrt(3))`
for not sliding
` F le mu mg , (mg )/(sqrt(3)) le mu mg `
` mu ge (1)/( sqrt(3))`
Promotional Banner

Topper's Solved these Questions

  • MOCK TEST 5

    VMC MODULES ENGLISH|Exercise PHYSICS ( SECTION-2)|5 Videos

  • MOCK TEST 4

    VMC MODULES ENGLISH|Exercise PHYSICS (SECTION 2)|5 Videos

  • MOCK TEST 6

    VMC MODULES ENGLISH|Exercise PHYSICS (SECTION 2)|5 Videos

Similar Questions

Explore conceptually related problems

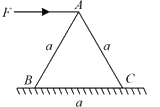
A horizontal force F is applied at the top of an equilateral triangular block having mass m . The minimum coefficient of friction required to topple the block before translation will be

force F is applied at the topmost point of block of mass M. The force required to topple the block before sliding is (µ = coefficient of friction)

A cubical box of side length L rests on a rough horizontal surface having coefficient of friction mu . A variable horizontal force F=alpha t is applied on the top of the block as shown in figure, where alpha is a constant and t is time. The coefficient of friction is sufficient so that the block does not slide before toppling. The graph between torque due to normal reaction about end B and time before toppling start is

A cubical box of side L rests on a rough horizontal surface with coefficient of friction p. A horizontal force F is a applied on the block as shown in Fig. 15.4.6. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

A cubical block of edge length 1 m and density 800 kg m^-3 rests on a rough horizontal surface with coefficient of friction mu . A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 ms^-2 ]

Find value of pulling force F for which block just moves. Given coefficient of friction for surface is mu .

An equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction mu . A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is

Two block , with masses m_(1) and m_(2) are staked as shown in fig and placed on a frictionless horizontal surface . There is a friction between the two block .An external force of magnitude F is applied to the top block at an angle alpha below the horizontal . The coefficient of friction between m_(1) and m_(2) are mu_(s) b. If the two blocks move together, find their acceleration b . Calculate the maximum value of force so that blocks will move together

A block of mass m is at rest on an inclined plane. The coefficient of static friction is mu . The maximum angle of incline before the block begins to slide down is :

Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is mu .