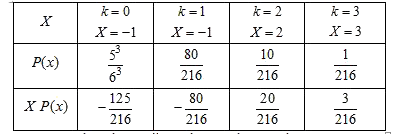A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-MOCK TEST 12-MATHEMATICS (SECTION 2)
- An unbiased die is tossed 3 times, suppose that a variable x is assign...
Text Solution
|
- lim(x to 2) (2^(x) + 2^(2 -x) - 5)/((1)/(sqrt(2^(x))) + lambda (2)^(1 ...
Text Solution
|
- If the sum of coefficients of all even powers in the expansion of (1 ...
Text Solution
|
- If the variance of first lambda + 1 natural numbers is 10 and varianc...
Text Solution
|
- Let A(3,4) B(5,0), C(0,5) be the vertices of a triangle ABC then orth...
Text Solution
|
- Let S be the set of point where the function f (x) = |4 - |2 - x|| is ...
Text Solution
|