A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-JEE MAIN - 5-PART I : PHYSICS (SECTION - 2)
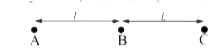
- Three particles A, B and C of mass m, m and 2m lie in a straight line ...
Text Solution
|
- An ice-breg of density 900 kgm^(-3) is floating in water of density 10...
Text Solution
|
- A sphere is made of an alloy of Metal A (density 8 g//cm^(3)) and Meta...
Text Solution
|
- A cylindrical tube with a frictionless piston ends in a small hole of ...
Text Solution
|
- A bullet of mass 50g if fired from below into the bob of mass 450g of ...
Text Solution
|
- A big particle of mass (3+m) kg blasts into 3 pieces , such that a par...
Text Solution
|