A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
PERMUTATIONS AND COMBINATIONS
OBJECTIVE RD SHARMA ENGLISH|Exercise Section I - Solved Mcqs|111 VideosPERMUTATIONS AND COMBINATIONS
OBJECTIVE RD SHARMA ENGLISH|Exercise Section II - Assertion Reason Type|9 VideosPARABOLA
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|30 VideosPROBABILITY
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|45 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA ENGLISH-PERMUTATIONS AND COMBINATIONS-Chapter Test
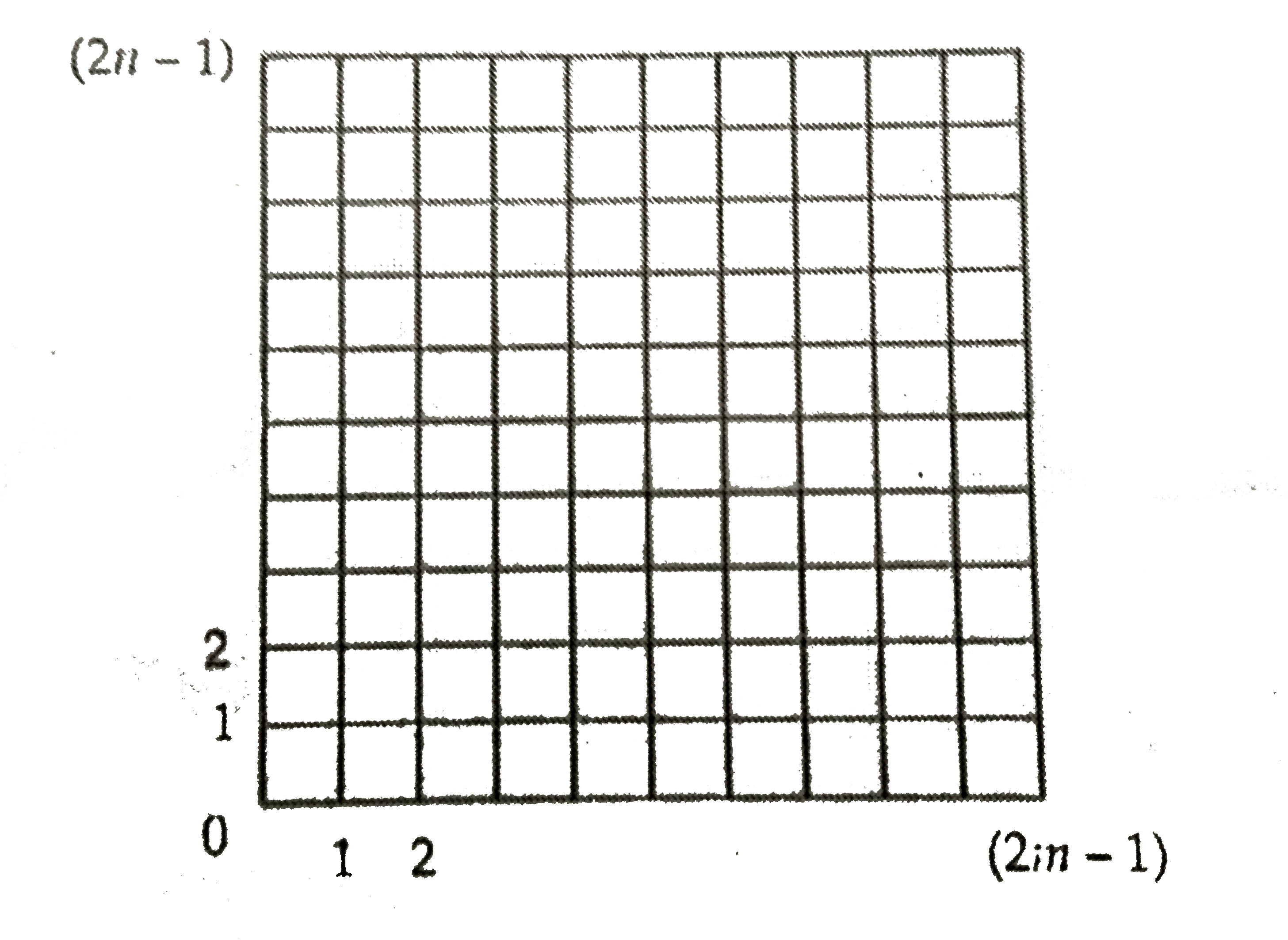
- A rectangle with sides 2m-1a n d2n-1 is divided into squares of uni...
Text Solution
|
- 7 women and 7 men are to sit round a circulartable such that there is ...
Text Solution
|
- There are (n+1) white and (n+1) black balls, each set numbered 1ton...
Text Solution
|
- 12 persons are to be arranged to a round table. If two particular pers...
Text Solution
|
- The number of committees of 5 persons consisting of at least one femal...
Text Solution
|
- The number of ways in which a team of eleven players can be selected f...
Text Solution
|
- In a football championship, 153 matches were played. Every two-team pl...
Text Solution
|
- How many numbers between 5000 and 10,000 can be formed using the digit...
Text Solution
|
- If x, y and r are positive integers, then ""^(x)C(r)+""^(x)C(r-1)+""^(...
Text Solution
|
- In how many ways can 5 red and 4 white balls be drawn from a bag conta...
Text Solution
|
- All the letters of the word 'EAMCET' are arranged in all possible ways...
Text Solution
|
- There are 10 lamps in a hall. Each one of them can be switched on i...
Text Solution
|
- How many 10-digit numbers can be formed by using digits 1 and 2
Text Solution
|
- The straight lines I(1),I(2),I(3) are parallel and lie in the same pla...
Text Solution
|
- about to only mathematics
Text Solution
|
- The number of diagonals that can be drawn by joining the vertices of a...
Text Solution
|
- The sum of the digits in unit place of all the numbers formed with the...
Text Solution
|
- In an examinations there are three multiple choice questions and each ...
Text Solution
|
- There are 10 points in a plane, out of these 6 are collinear. If N is ...
Text Solution
|
- Ramesh has 6 friends. In how many ways can be invite one or more of th...
Text Solution
|
- If Pm stands for ^m Pm , then prove that: 1+1. P1+2. P2+3. P3++ndotPn=...
Text Solution
|