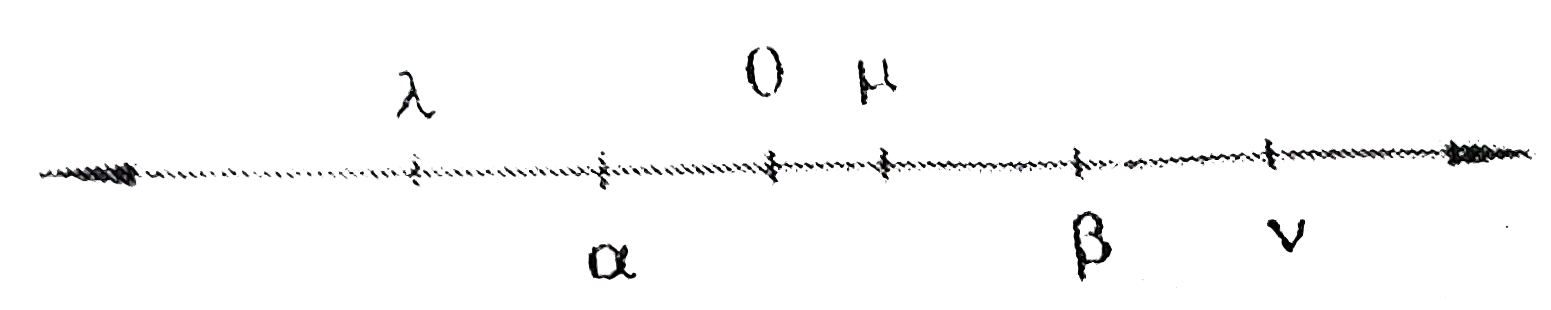A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MAXIMA AND MINIMA
OBJECTIVE RD SHARMA ENGLISH|Exercise Section II - Assertion Reason Type|7 VideosMAXIMA AND MINIMA
OBJECTIVE RD SHARMA ENGLISH|Exercise Exercise|47 VideosMAXIMA AND MINIMA
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|29 VideosMATHEMATICAL REASONING
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|20 VideosMEASURES OF CENTRAL TENDENCY
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|21 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA ENGLISH-MAXIMA AND MINIMA -Section I - Solved Mcqs
- The minimum value of the fuction f(x) given by f(x)=(x^m)/(m)+(x^(-...
Text Solution
|
- The largest term in the sequence an=(n^2)/(n^3+200) is given by (529)/...
Text Solution
|
- Let f(x)=ax^3+bx^2+cx+1 has exterma at x=alpha,beta such that alpha ...
Text Solution
|
- P=x^3-1/x^3, Q=x-1/x x in (1,oo) then minimum value of P/(sqrt(3)Q^2...
Text Solution
|
- Let f(x)=cos2pix+x-[x]([,] denote the greatest integer function). Then...
Text Solution
|
- Let f(x)=a-(x-3)^(8//9) then greatest value of f(x) is
Text Solution
|
- A function f such that f'(a)=f''(a)=….=f^(2n)(a)=0 , and f has a l...
Text Solution
|
- Let f(x)={{:(3x^2-2x+10, x lt 1),(-2,x gt 1):} The set of values of ...
Text Solution
|
- The maximum value of cos (int(2x)^(x^(2)) e^t sin^2 " t dt ")
Text Solution
|
- Let f (x)= {{:(1+ sin x "," , x lt 0),( x ^(2) -x+1",", x ge 0):}, the...
Text Solution
|
- Let f(x)=x^(n+1)+ax^n, "where " a gt 0. Then, x=0 is point of
Text Solution
|
- The greph of y=x^3+ax^2+bx+c has no extemun if and only if
Text Solution
|
- If f(x) =underset(x)overset(x^2)int(t-1)dt, 1 le x le 2 then the great...
Text Solution
|
- If the parabola y=ax^2+bx+c has vertex at(4,2)and a in [1,3] then the...
Text Solution
|
- Let f(x)=In (2x-x^(2))+"sin"(pix)/(2). Then
Text Solution
|
- Find a quadratic polynomial varphi(x) whose zeros are the maximum ...
Text Solution
|
- Let f(x)={{:(x^2+4x "," -3 le x le 0),(-sin x ","0 lt x le pi//2 ),(...
Text Solution
|
- If alpha be the number of solutions of the equation [sin x] =|x| ) and...
Text Solution
|
- Let f(x1,x2,x3,x4)=x1^2+x2^2+x3^2+x4^2-2(x1+x2+x3+x4)+10 and x1,x3 i...
Text Solution
|
- Let f,g and h be real-valued functions defined on the interval [0,1] b...
Text Solution
|