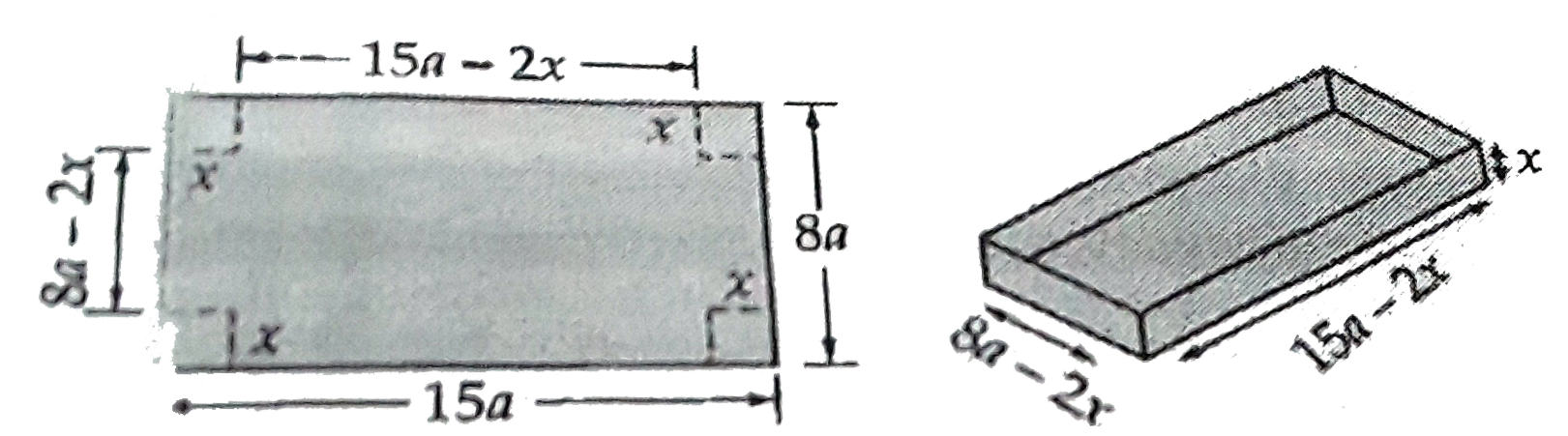
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MAXIMA AND MINIMA
OBJECTIVE RD SHARMA ENGLISH|Exercise Section II - Assertion Reason Type|7 VideosMAXIMA AND MINIMA
OBJECTIVE RD SHARMA ENGLISH|Exercise Exercise|47 VideosMAXIMA AND MINIMA
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|29 VideosMATHEMATICAL REASONING
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|20 VideosMEASURES OF CENTRAL TENDENCY
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|21 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA ENGLISH-MAXIMA AND MINIMA -Section I - Solved Mcqs
- Find a quadratic polynomial varphi(x) whose zeros are the maximum ...
Text Solution
|
- Let f(x)={{:(x^2+4x "," -3 le x le 0),(-sin x ","0 lt x le pi//2 ),(...
Text Solution
|
- If alpha be the number of solutions of the equation [sin x] =|x| ) and...
Text Solution
|
- Let f(x1,x2,x3,x4)=x1^2+x2^2+x3^2+x4^2-2(x1+x2+x3+x4)+10 and x1,x3 i...
Text Solution
|
- Let f,g and h be real-valued functions defined on the interval [0,1] b...
Text Solution
|
- Let f be a function defined on R (the set of all real numbers) such th...
Text Solution
|
- Let f:""RvecR be defined by f(x)""={k-2x , if""xlt=-1 2x+3,f""x >-1} ....
Text Solution
|
- For x epsilon(0,(5pi)/2), definite f(x)=int(0)^(x)sqrt(t) sin t dt. T...
Text Solution
|
- Let p(x) be a real polynomial of least degree which has a local maximu...
Text Solution
|
- Let I RvecI R be defined as f(x)=|x|++x^2-1|dot The total number of po...
Text Solution
|
- If f(x) = underset(0)overset(x)inte^(t^(2)) (t-2) (t-3) dt for all x ...
Text Solution
|
- The funciton f(X) =2|x|+|x+2|-||x+2|-|x|| has a local mimimum or a lo...
Text Solution
|
- Let f:[0,1]rarrR be a function. Suppose the function f is twice differ...
Text Solution
|
- Let f:[0,1] rarr R be a function.such that f(0)=f(1)=0 and f''(x)+f(x...
Text Solution
|
- A rectangular sheet of fixed perimeter with sides having their lengths...
Text Solution
|
- Let f(X) be a polynomila of degree four having extreme values at x =1 ...
Text Solution
|
- A cylindrical container is to be made from certain solid material with...
Text Solution
|
- The minimum value of the function, f(x)=x^(3//2)+x^(-3//2)-4(x+(1)/(...
Text Solution
|
- The least value of alpha in R for which 4ax^2+(1)/(x)ge1, for all xgt ...
Text Solution
|
- The abscissae of a point, tangent at which to the curve y = e^x sin x...
Text Solution
|