Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PSEB-AREAS OF PARALLELOGRAMS AND TRIANGLES-EXAMPLE
- In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC mee...
Text Solution
|
- In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, A...
Text Solution
|
- If a triangle and a parallelogram are on the same base and between sam...
Text Solution
|
- Show that a median of a triangle divides it into two triangles of equa...
Text Solution
|
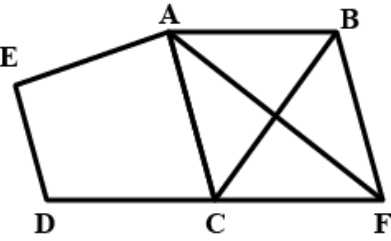
- In Fig. 9.22, ABCD is a quadrilateral and BE || AC and also BE meets D...
Text Solution
|