Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PSEB-CIRCLES-EXAMPLE
- Given an arc of a circle, complete the circle.
Text Solution
|
- If two intersecting chords of a circle make equal angles with the diam...
Text Solution
|
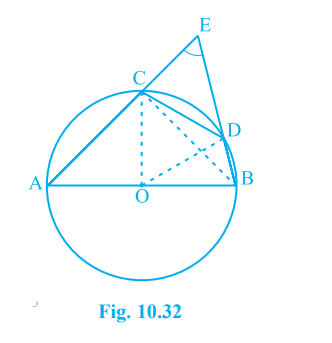
- In Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to ...
Text Solution
|
- In Fig 10.33, ABCD is a cyclic quadrilateral in which AC and BD are it...
Text Solution
|
- Two circles intersect at two points A and B. AD and AC are diameters t...
Text Solution
|
- Prove that the quadrilateral formed (if possible) by the internal angl...
Text Solution
|