Text Solution
Verified by Experts
Topper's Solved these Questions
CO-ORDINATE GEOMETRY
NAGEEN PRAKASHAN ENGLISH|Exercise Problems From NCERT/ Exemplar|6 VideosCO-ORDINATE GEOMETRY
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise|8 VideosCIRCLE
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (long Answer Questions )|5 VideosCONSTRUCTIONS
NAGEEN PRAKASHAN ENGLISH|Exercise EXERCISE|36 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-CO-ORDINATE GEOMETRY -Exercise
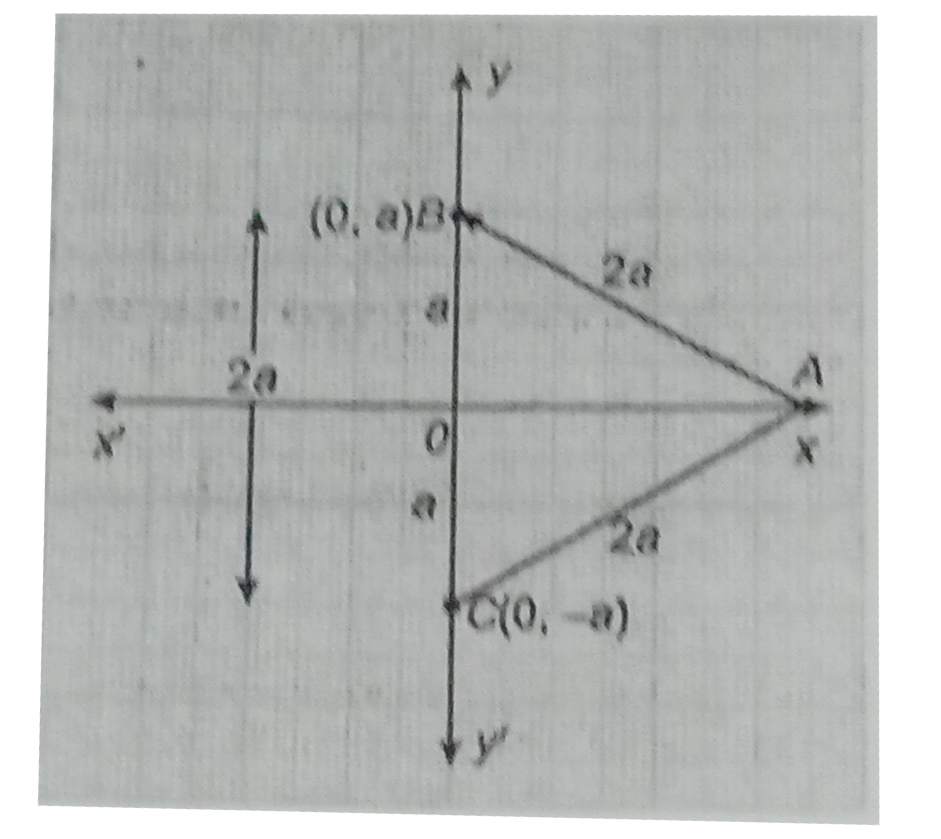
- The base f an equilateral triangle with side 2a lies along the y-ax...
Text Solution
|
- Plot the following points on the same graph paper : (i) (7,6) (ii)...
Text Solution
|
- Use the given graph to find the co-ordinates of the points, satisfying...
Text Solution
|
- In each of the following the co-ordinates of the three vertices of a r...
Text Solution
|
- In which quadrant does the given points lie (i) (4,-2) (ii) (-2,-2...
Text Solution
|
- A(-2,2),B(8,2) and C(4,-4) are the vertice of a parallelogram ABCD. By...
Text Solution
|
- A (-2,4) , C (4,10) and D (-2,10) are the vertices of a square ABCD. ...
Text Solution
|
- Plot the point A(4,4) on a graph paper. Draw perpendicular AP on x-axi...
Text Solution
|
- Find the mirror image of the point A(-3,2) in x-axis.
Text Solution
|