(i) In `triangleADB and triangleBDC`
`{:(angle5=angle4 " "("each "90^(@)),|,"Searching for second Angles"),(,"We know that " angle1+angle2=90^(@).....(1),),(,"Also, Since " angle4=90^(@),),(,:. " " angle2+angle3=90^(@),),(," (angle sum property)...(2)",),(,:. "From (1) and (2) , We get " ,),(,rArr " " angle1+angle2=angle2+angle3 " "(each 90^(@)),),(,rArr " " angle1=angle3,):}`
` angle1 = angle3` ( just proved)
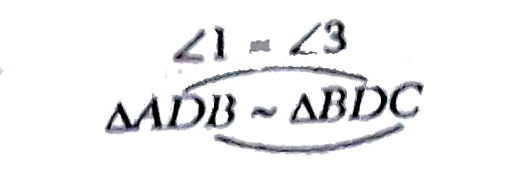
(AA corollary) Hence proved.
(ii) `triangle BDC and triangleABC`
`angle4= angle1+angle2 ("each" 90^(@))`
` angle3= angle3` ( common)

(AA corollary) Hence poved.
(iii) In `triangleBDC and trinangleABC`
`angle4= angle1+angle2 ( "each" 90^(@))`
`angle3=angle3 ` (common)

[from part (i)
(corresponding sides of similar triangles are proportional)
(iv) For `BD^(2)= AD xx DC` . we need to prove two `triangles` similar which contain BD, AD and DC as sides.
Obviosly these are `triangleABD and triangleBDC`, we have proved these `triangles` as similar in part (i). so ,
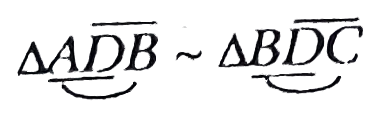
[from part (ii)]
( corresponding sides of similar triangle are proportional)
`BD^(2)= ADxx DC` Hence proved.
(v) For ` AB^(2)= AD xx AC` we need to prove two triangles similar which contain AB, AD and AC as sides. Obviosusly these are `triangleABD and triangleABC`. we have already proved these `triangles` as similar in part (ii)
` triangleADB ~ triangleABC` [ from part (ii) ]
` Rightarrow AB^(2)= ADxx AC` .... (1) Hence proved
(vi) For `BC^(2)= CDxxAC` we need to prove two triangles similar which contains BC, CD and AC as sides. Obviosly these are `triangleBDC and triangleABC` , we have proved these triangles as similar in part (iii)
so,
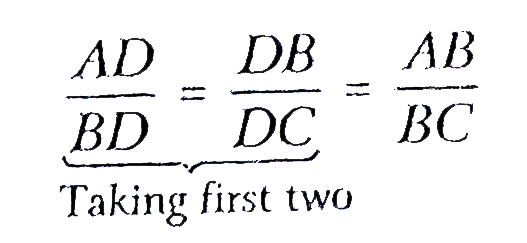
( cossesponding sides of similar triangle are proportional)
`BC^(2) = CD xx AC` ....(2) Hence proved.
(vii) Addings results (1) and (2), we get
`AB^(2)+BC^(2)= ADxxAC+CDxxAC`
`AC ( AD + CD)
= AC xx AC = AC^(2)` Hence proved.

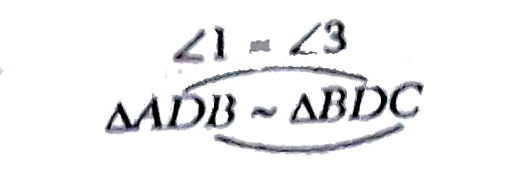 (AA corollary) Hence proved.
(AA corollary) Hence proved.  (AA corollary) Hence poved.
(AA corollary) Hence poved. [from part (i)
[from part (i) 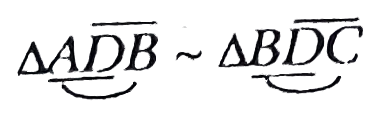 [from part (ii)]
[from part (ii)] 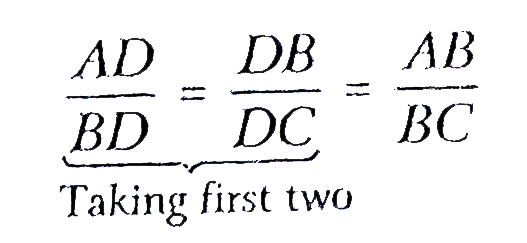 ( cossesponding sides of similar triangle are proportional)
( cossesponding sides of similar triangle are proportional)