A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise (Multiple)|17 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise (Reasoning Questions)|10 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise SUBJECTIVE TYPE|1 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE|Exercise Question Bank|12 VideosTRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
CENGAGE|Exercise Question Bank|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-THREE-DIMENSIONAL GEOMETRY -Exercise (Single)
- Shortest distance between the lines (x-1)/1=(y-1)/1=(z-1)/1a n d(x-...
Text Solution
|
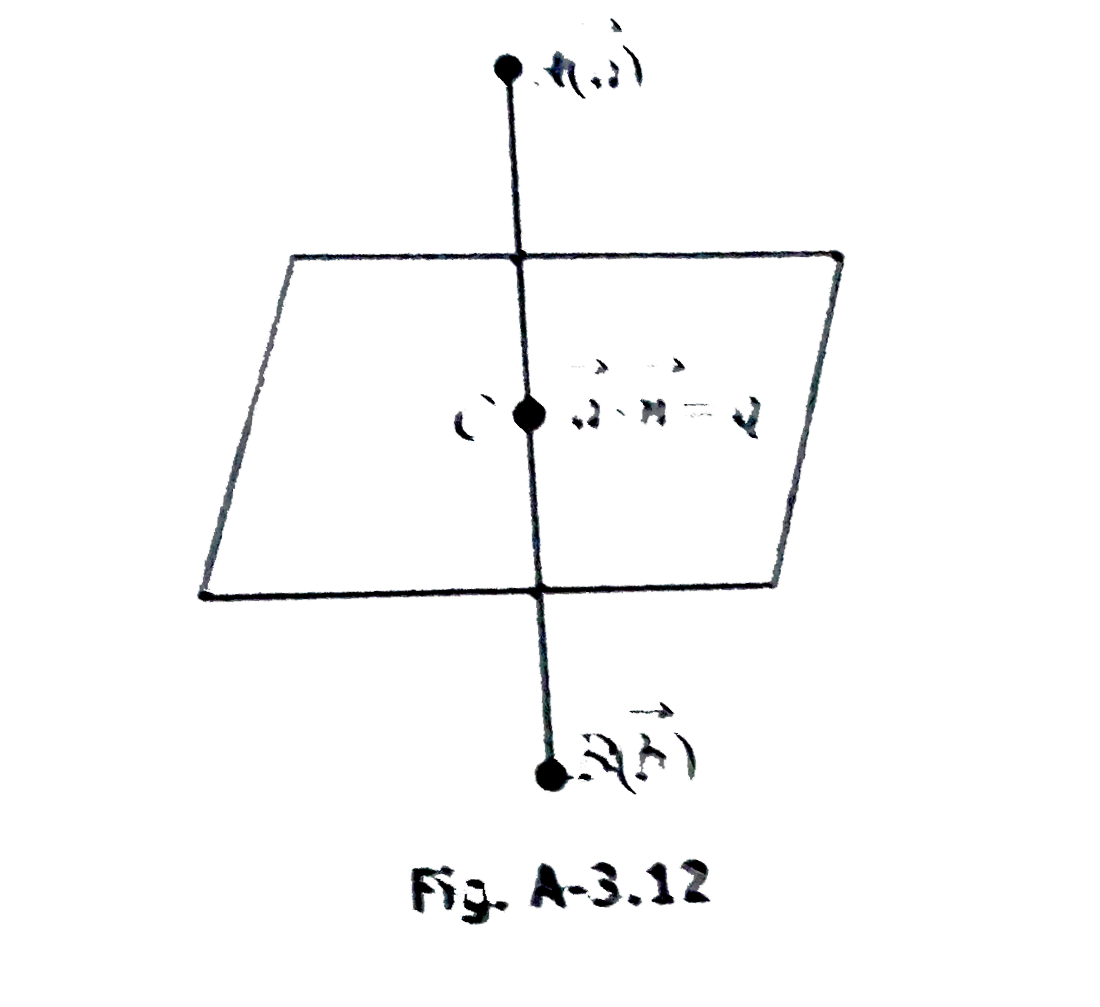
- Distance of point P(vecP) from the plane vecr.vecn=0 is
Text Solution
|
- The reflection of the point veca in the plane vecr.vecn=q is (A) veca+...
Text Solution
|
- The angle theta between the line vecr=veca+lambdavecb and the plane ve...
Text Solution
|
- If a line makes an angel of pi/4 with the positive direction of eac...
Text Solution
|
- The ratio in which the plane vec rdot( vec i-2 vec j+3 vec k)=17 d...
Text Solution
|
- then image of the point (-1,3,4) in the plane x-2y=0
Text Solution
|
- The perpendicular distance between the line vecr = 2hati-2hatj+3hatk+l...
Text Solution
|
- Let L be the line of intersection of the planes 2x+3y+z=1a n dx+3y+2z=...
Text Solution
|
- The length of the perpendicular drawn from (1,2,3) to the line (x-6...
Text Solution
|
- If the angle theta between the line (x+1)/1=(y-1)/2=(z-2)/2 and the pl...
Text Solution
|
- The intersection of the spheres x^2+y^2+z^2+7x-2y-z=13a n dx^2+y^2=...
Text Solution
|
- If a plane cuts off intercepts OA = a, OB = b, OC = c from the coordi...
Text Solution
|
- A line makes an angel theta with each of the x-and z-axes. If the a...
Text Solution
|
- The shortest distance from the plane 12 x+y+3z=327 to the sphere x^...
Text Solution
|
- A tetrahedron has vertices O(0,0,0),A(1,2,1),B(2,1,3),a n dC(-1,1,2), ...
Text Solution
|
- The radius of the circle in which the sphere x^(I2)+y^2+z^2+2z-2y-4...
Text Solution
|
- The lines (x-2)/1=(y-3)/2=(z-4)/(-k)a n d=(x-1)/k=(y-4)/2=(z-5)/1 are ...
Text Solution
|
- The point of intersection of the lines (x-5)/3=(y-7)/(-1)=(z+2)/1a ...
Text Solution
|
- Two systems of rectangular axes have the same origin. If a plane cu...
Text Solution
|