Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-LIMITS-Question Bank
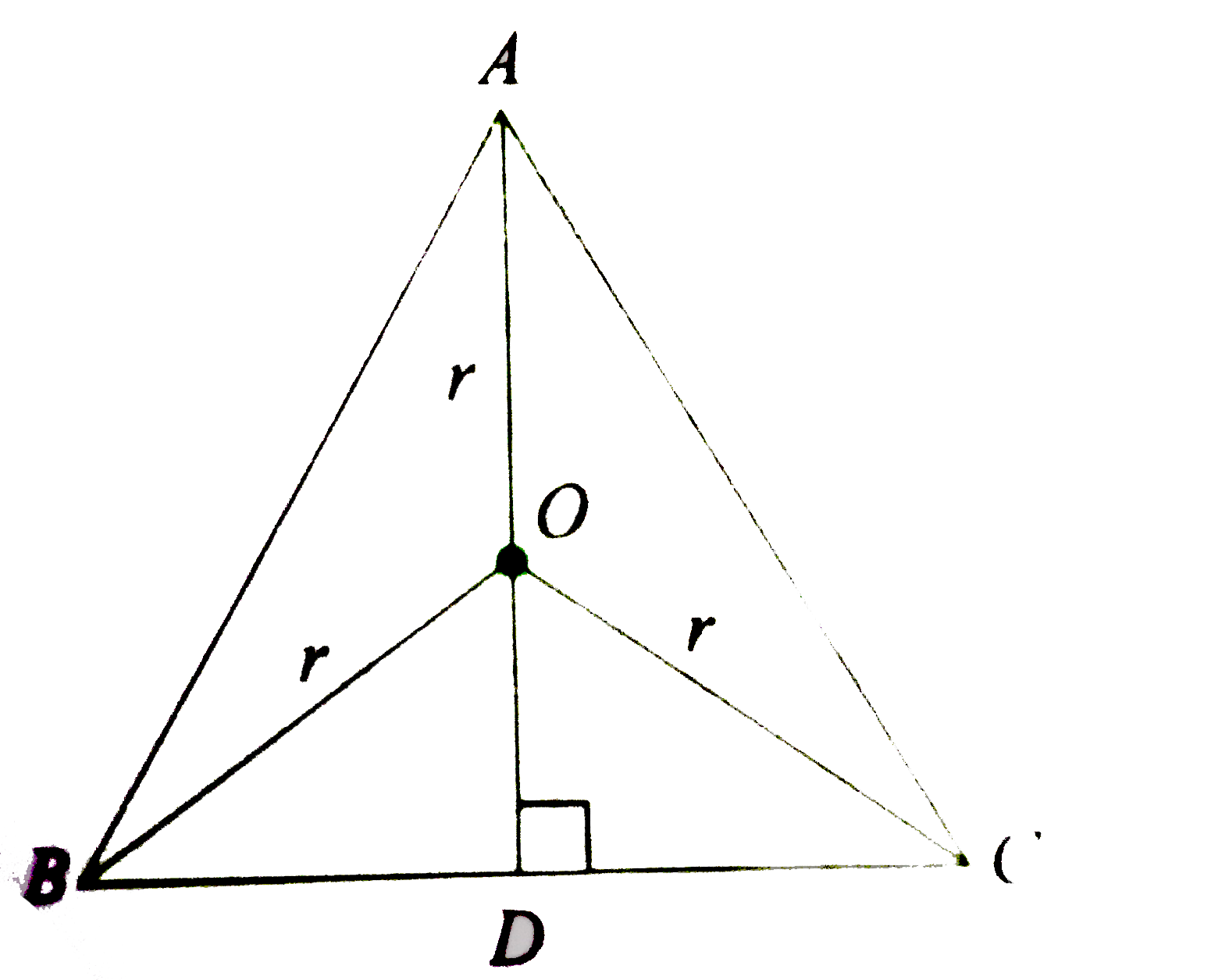
- ABC is an isosceles triangle inscribed in a circle of radius rdot If A...
Text Solution
|
- If Lim(x rarr 0) (1-cosx)/(e^(ax)-bx-1) exist and is equal to 1, then ...
Text Solution
|
- If graph of a function f(x) is shown in the adjacent figure, then Lim(...
Text Solution
|
- Let f(x) =(sec x)^(cosecx) + (cot x)^(sin x). Then the value of Lim(x ...
Text Solution
|
- Lim(z rarr 0){{max((sin^(-1)x + cos^(-1)x)^(2), min(x^(2)+4x+7))}. (si...
Text Solution
|
- The reciprocal of the value of: ("lim")(ntooo)(1-1/(2^2))(1-1/(3^2))(1...
Text Solution
|
- The value of Lim(x rarr 0)(sum(k =1)^(2016){(sinx)/x+2015k})/2016 is [...
Text Solution
|
- Lim(x rarr oo) (30+4sqrtx+7root(3)(x))/(2+sqrt(4x-7)+root(3)(6x-2) )eq...
Text Solution
|
- If Lim(x rarr0) ((a sin x + b tan x)/x^(3))= 3/2 then |a+2b| is equal ...
Text Solution
|
- lim(n rarr 0)(1/(1+n^(2))+2/(1+n^(2))+3/(1+n^(2))+....+n/(1+n^(2))) is...
Text Solution
|
- Find the value of lim(n rarr oo)sum(k=1)^(n)(k^(2)+k-1)/((k+1)!) .
Text Solution
|
- The value of Lim(x rarr 0)((tanx)^(1/x)+(1+sinx)^(x)) where x gt0 is e...
Text Solution
|
- If Lim(x rarr 0) (a sinx + bxe^(x)+3x^(2))/(sin x-2x+tanx) exists and ...
Text Solution
|
- If Lim(x rarr a) (sqrt(x-b)-sqrt(a-b))/(x^(2)-a^(2))(a gt b) = 1/64 an...
Text Solution
|
- If lim(x rarr 0) (k+cos lx)/x^(2)exists and has the value equal to -4 ...
Text Solution
|
- Lim(x rarr 0)((3sin x- sin 3x)^(4))/((sec x - cosx)^(6)) is equal to
Text Solution
|
- Lim(x rarr 0)(tanx sqrt (tanx)-sin x sqrt(sinx))/(x^(3).sqrtx) equals
Text Solution
|
- f(x)=("ln"(x^(2)+e^(x)))/("ln"(x^(4)+e^(2x)))." Then "underset(xtooo)l...
Text Solution
|