Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-MATRICES-Exercise 13.4
- If A and B are matrices of the same order, then A B^T-B A^T is a/an ...
Text Solution
|
- If A and B are square matrices such that AB = BA then prove that A^(3)...
Text Solution
|
- If A is a square matrix such that A^(2)= I, then (A-I)^(3)+(A+I)^(3)...
Text Solution
|
- If B ,C are square matrices of order na n difA=B+C ,B C=C B ,C^2=O , t...
Text Solution
|
- Let A be any 3xx2 matrix. Then prove that det. (A A^(T))=0.
Text Solution
|
- Let A be a matrix of order 3, such that A^(T)A=I. Then find the value ...
Text Solution
|
- A and B are different matrices of order n satisfying A^(3)=B^(3) and A...
Text Solution
|
- IfD=d i ag[d1, d2, dn] , then prove that f(D)=d i ag[f(d1),f(d2), ,f(...
Text Solution
|
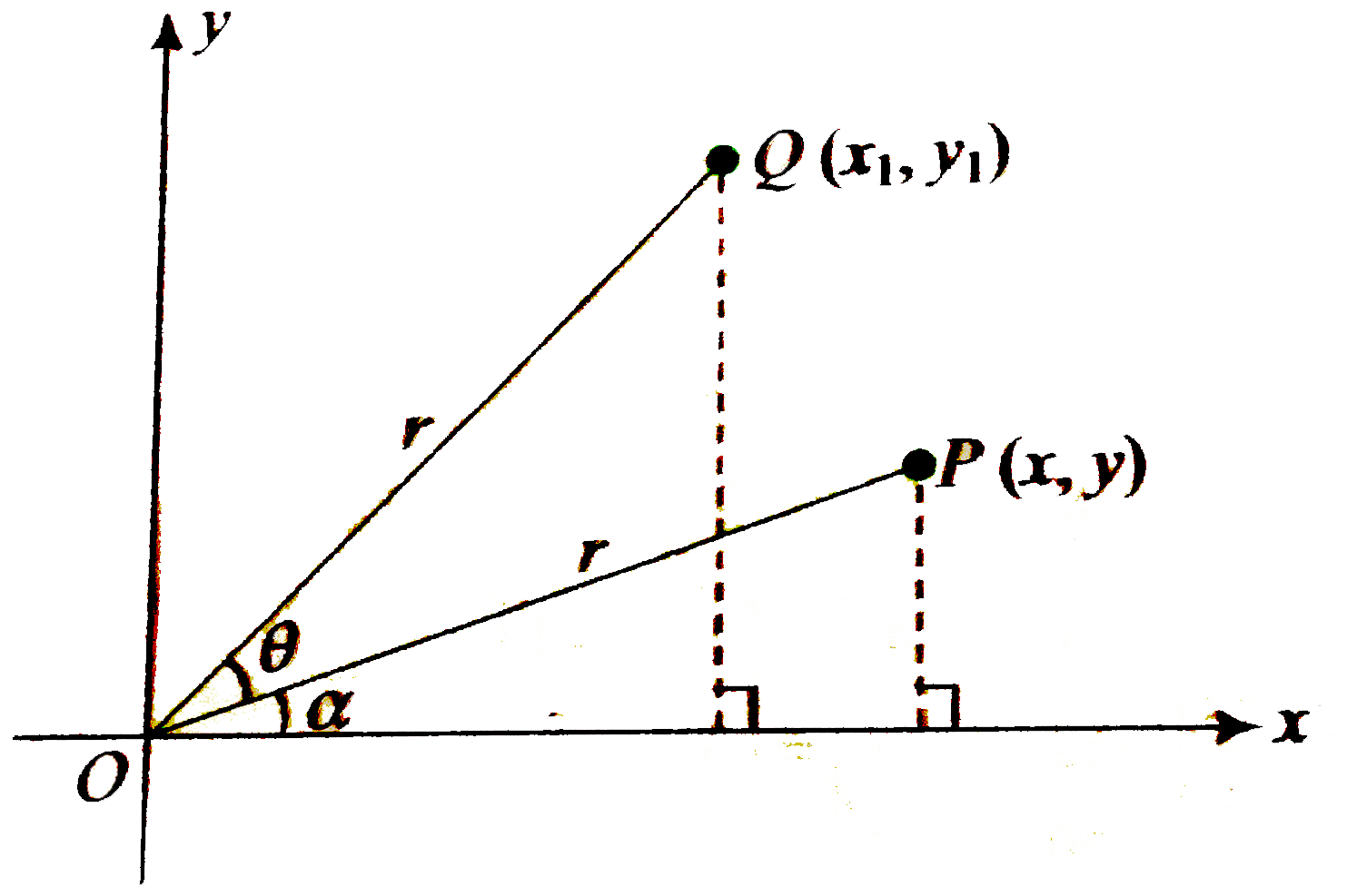
- Point P(x, y) is rotated by an angle theta in anticlockwise direction....
Text Solution
|
- How many different diagonal matrices of order n can be formed which ar...
Text Solution
|
- How many different diagonal matrices of order n can be formed which ar...
Text Solution
|
- If A and B are n-rowed unitary matrices,then AB and BA are also unitar...
Text Solution
|