Home
Class 12
MATHS
Let f:[0,4pi]vec[0,pi] be defined by f(x...

Let `f:[0,4pi]vec[0,pi]` be defined by `f(x)=cos^(-1)(cosx)dot` The number of points `x in [0,4pi]s a t i sfy ingt h e` equation `f(x)=(10-x)/(10)` is____

Text Solution

Verified by Experts

`f:[0,4opi]to[0,pi],f(x)m = cos^(-1)(cosx)`.
For the number of roots of th equation `cos^(-1) (cos x) = (10-x)/(10)` , draw the graph of `y=cos^(-1)(cos x)" and "y=(10-x)/(10)`and find the number points of intersections.

From the graph, the number of solution is 3.
Promotional Banner

Topper's Solved these Questions

  • GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE|Exercise Exercise|18 Videos

  • GETTING STARTED WITH GRAPHS

    CENGAGE|Exercise Exercise|18 Videos

  • GRAPHICAL TRANSFORMATIONS

    CENGAGE|Exercise Exercise|14 Videos

Similar Questions

Explore conceptually related problems

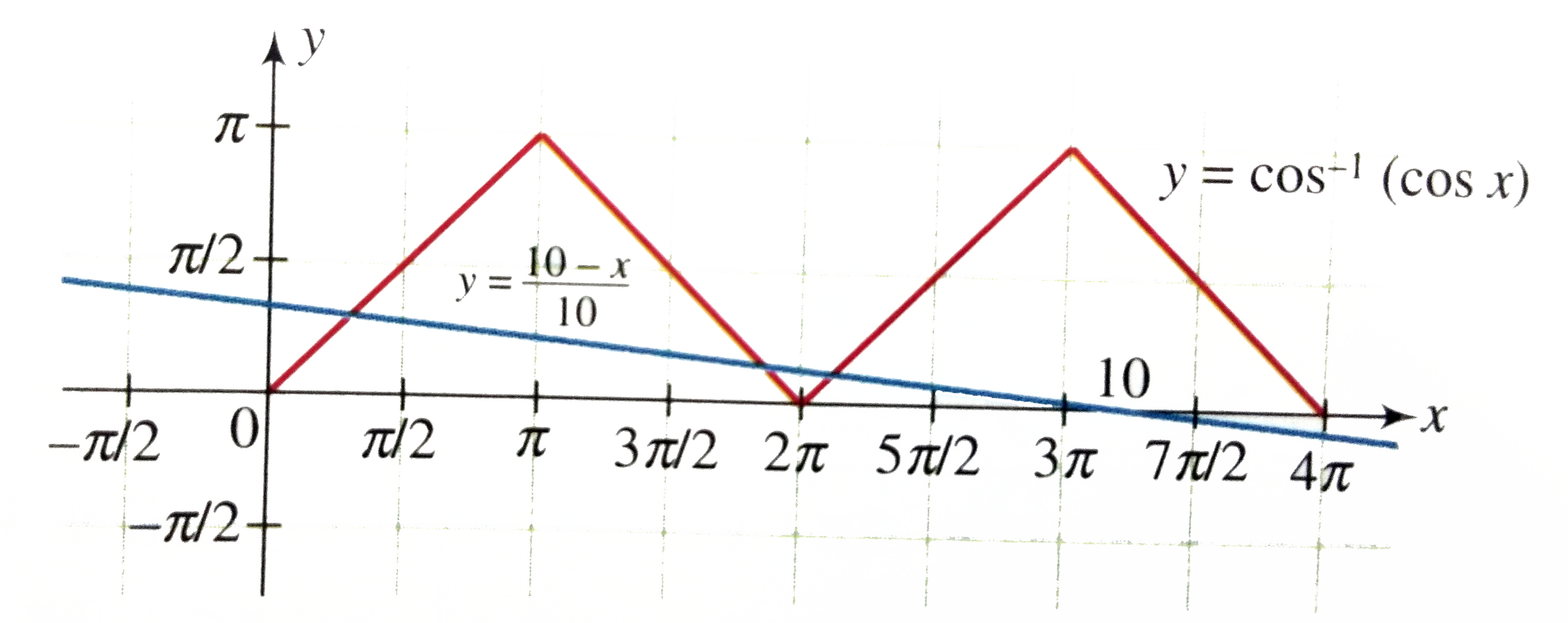
Let f:[0,4pi]->[0,pi] be defined by f(x)=cos^-1(cos x). The number of points x in[0,4pi] 4satisfying the equation f(x)=(10-x)/10 is

The number of solution of 2cosx=|sinx| where x in [0.4pi] is/are

Let f(x)=sin^(23)x-cos^(22)xa n dg(x)=1+1/2tan^(-1)|x| . Then the number of values of x in the interval [-10pi,8pi] satisfying the equation f(x)=sgn(g(x)) is __________

Let f(x)=sin^(23)x-cos^(22)xa n dg(x)=1+1/2tan^(-1)|x| . Then the number of values of x in the interval [-10pi,8pi] satisfying the equation f(x)=sgn(g(x)) is __________

Let a function f be defined by f(x)=(x-|x|)/x for x ne 0 and f(0)=2. Then f is

Let f: R ->[0,pi/2) be defined by f(x)=tan^(-1)(x^2+x+a)dot Then the set of values of a for which f is onto is (a) (0,oo) (b) [2,1] (c) [1/4,oo] (d) none of these

The number of roots of the equation sin(2x+pi/18) cos(2x-pi/9)=-1/4 in [0, 2pi] is

If x in (0,pi//2) , then the function f(x)= x sin x +cosx +cos^(2)x is