Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercise
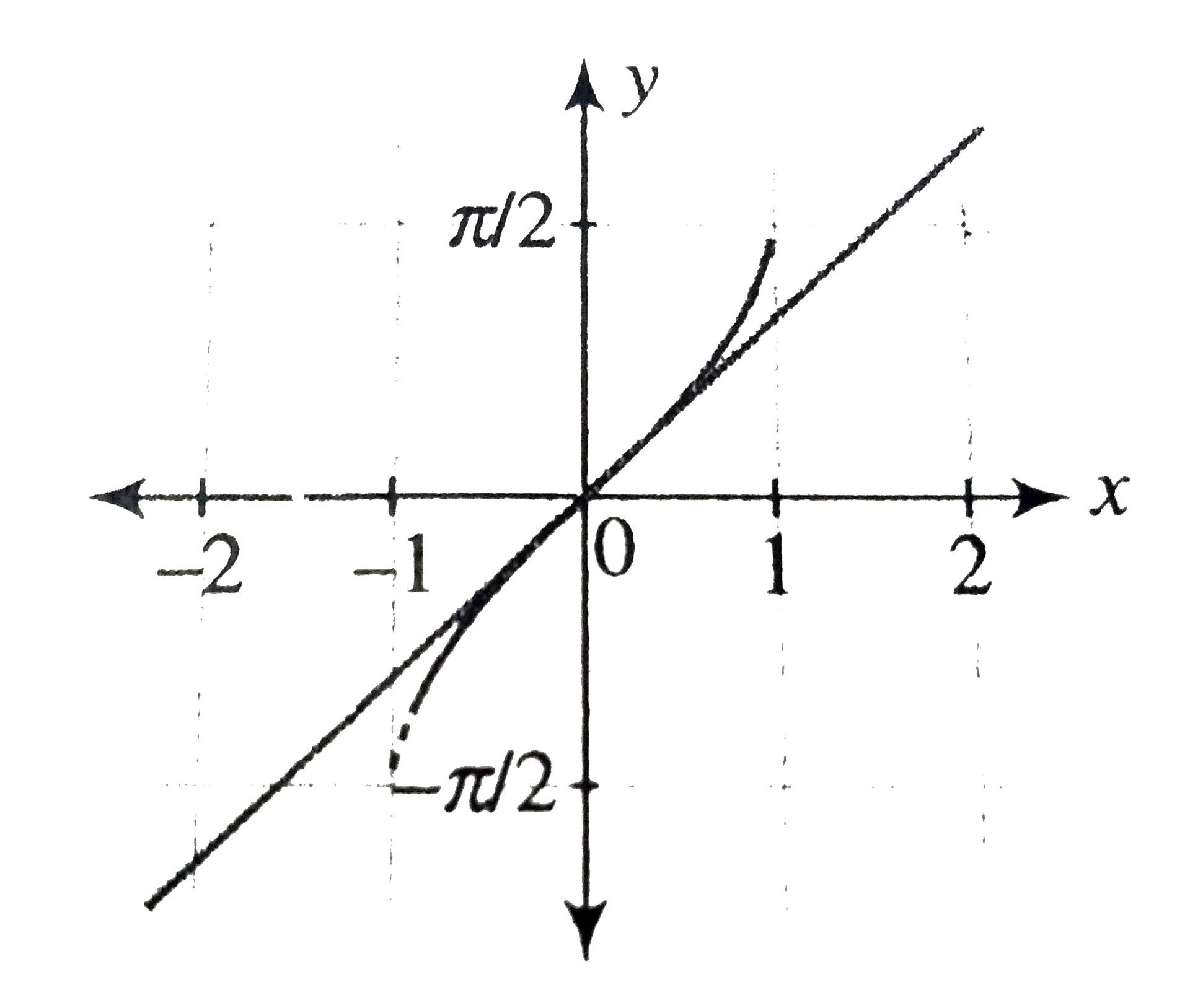
- Draw the graph of y=tan^(-1)x+cot^(-1)x
Text Solution
|
- Find the number of real solutions to the equation log(0.5)x=|x|.
Text Solution
|
- Prove that [underset(xto0)lim(sinx)/(x)]=0, where [.] represents the g...
Text Solution
|
- Solve tan^(-1) x gt cot^(-1) x
Text Solution
|
- Match the following Column I to Column II
Text Solution
|
- Draw the graph of y=cos^(-1)(x%+^(2)).
Text Solution
|
- Find the value of int(0)^(100pi)sin^(-1)(sin x)dx.
Text Solution
|
- Draw the graph of y=sin^(-1)(x-3).
Text Solution
|
- Draw the graph of y=cos^(-1)(x%+^(2)).
Text Solution
|
- Draw the graph of y=cot^(-1)x.
Text Solution
|
- Draw the graph of y=cos^(-1)(x%+^(2)).
Text Solution
|
- Draw the graph of y=cos^(-1){x}," where "{*}" represetns the fractiona...
Text Solution
|
- If f(x) = 0 has n roots, then f'(x) = 0 has ………..roots
Text Solution
|
- Draw the graph of f(x)=[cot^(-1)x]," where "[*] represents the greate...
Text Solution
|
- Draw the graph of y=|x|.
Text Solution
|
- Draw the graph of y=-cot^(-1)x.
Text Solution
|
- Draw the graph of y=sin^(-1)(x-3).
Text Solution
|
- Draw the graph of y=tan^(-1)|x|.
Text Solution
|