Home
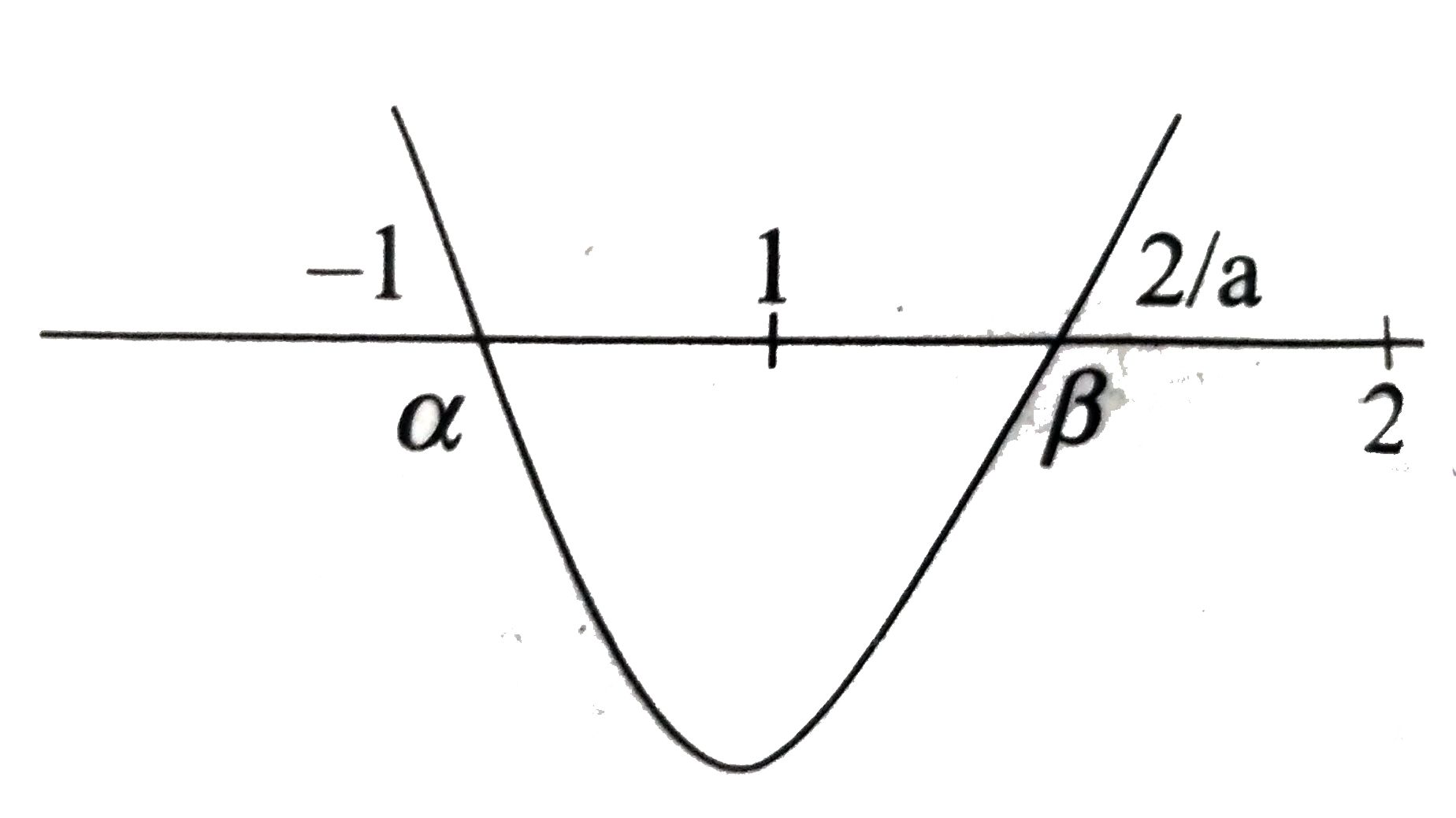
Class 12
MATHS
The set of values of a for which a x^2+(...

The set of values of `a` for which `a x^2+(a-2)x-2` is negative for exactly two integral `x ,` is `(0,2)` b. `[1,2)` c. `(1,2]` d. `(0,2]`

A

`[-1,1]`

B

`[1,2)`

C

`[-1,1]`

D

`[-2,-1])

Text Solution

Verified by Experts

The correct Answer is:
B
`(b)` Let `f(x)=ax^(2)+(a-2)x-2`
`f(x)` is negative for two integral values of `x`, so graph should be vertically upward parabola
i.e., `a gt 0`
Let two roots of `f(x)=0` are `alpha` and `beta`, then
`alpha`, `beta=(-a(a-2)+-(a+2))/(2a)`
`impliesa=-1`, `beta=(2)/(a)`
`implies1 lt beta le 2`
`implies 1 lt (2)/(a) le 2`
`implies a in [1,2)`
Promotional Banner

Topper's Solved these Questions

  • THEORY OF EQUATIONS

    CENGAGE|Exercise Comprehension|12 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise Multiple Correct Answer|6 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise JEE Advanced Previous Year|4 Videos

  • THREE DIMENSIONAL GEOMETRY

    CENGAGE|Exercise Question Bank|12 Videos

Similar Questions

Explore conceptually related problems

The set of values of a for which a x^2+(a-2)x-2 is negative for exactly two integral x , is a. (0,2) b. [1,2) c. (1,2] d. (0,2]

All the values of ' a ' for which the quadratic expression a x^2+(a-2)x-2 is negative for exactly two integral values of x may lie in [1,3/2] (b) [3/2,2) [1,2) (d) [-1,2)

If set of values a for which f(x)=a x^2-(3+2a)x+6, a!=0 is positive for exactly three distinct negative integral values of x is (c , d] , then the value of (c^2 + 4|d|) is equal to ________.

The set of all values of x for which ((x+1)(x-3)^(2)(x-5)(x-4)^(3)(x-2))/(x) lt 0

The set of value(s) of a for which the function f(x)=(a x^3)/3+(a+2)x^2+(a-1)x+2 possesses a negative point of inflection is (-oo,-2)uu(0,oo) (b) {-4/5} (-2,0) (d) empty set

Number of integral values of a for which the equation x^2-(a+1)x+a-1=0 , has integral roots, is equal to -

The exhaustive set of values of a for which inequation (a -1)x^2- (a+1)x+ a -1>=0 is true AA x >2 (a) (-oo,1) (b)[7/3,oo) (c) [3/7,oo) (d) none of these

The number of values of a for which equations x^3+a x+1=0a n d x^4+a x^2+1=0 have a common root is a. 0 b. 1 c. 2 d. Infinite

The number of integral values of a for which the quadratic equation (x+a)(x+1991)+1=0 has integral roots are a. 3 b. 0 c. 1 d. 2

The number of value of k for which [x^2-(k-2)x+k^2]xx""[x^2+k x+(2k-1)] is a perfect square is a. 2 b. 1 c. 0 d. none of these