A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-STRAIGHT LINE-Multiple Correct Answers Type
- The point P(alpha,alpha +1) will lie inside the triangle whose vertice...
Text Solution
|
- A straight line passing through the point A(-2,-3) cuts lines x +3y = ...
Text Solution
|
- If A(3,4) and B(-5,-2) are the extremities of the base of an isosceles...
Text Solution
|
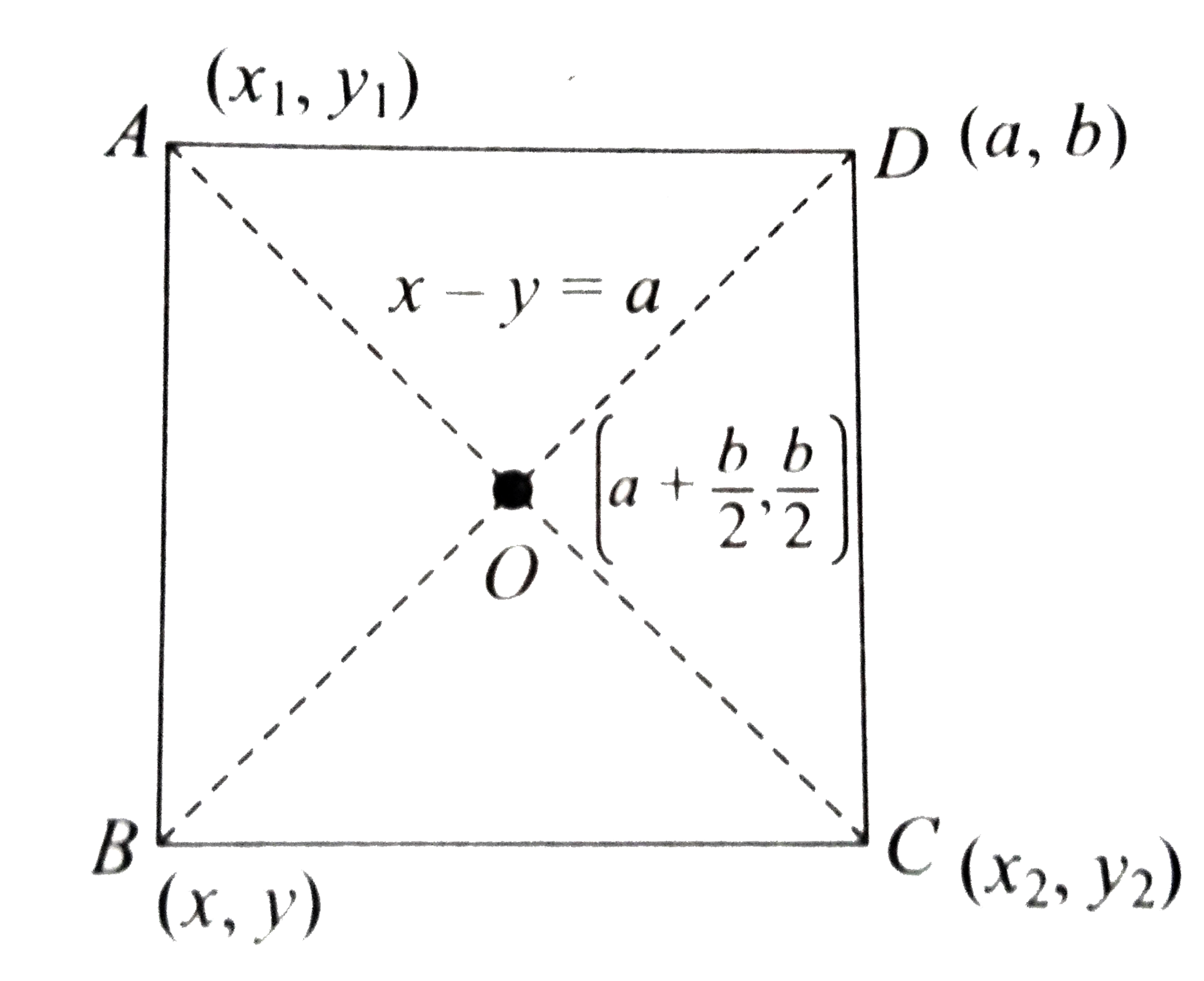
- If (a, b) be an end of a diagonal of a square and the other diagonal ...
Text Solution
|
- The equation of the diagonals of a rectangle are y+8x-17=0 and y-8x+7=...
Text Solution
|
- If 6a^2-3b^2-c^2+7ab-ac+4bc=0 then the family of lines ax+by+c=0,|a|+...
Text Solution
|
- If graph of xy = 1 is reflected in y = 2x to give the graph 12x^(2) +r...
Text Solution
|
- Let A,B,C be angles of triangles with vertex A -= (4,-1) and internal ...
Text Solution
|