Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-CIRCLE -MATRIX MATCH TYPE
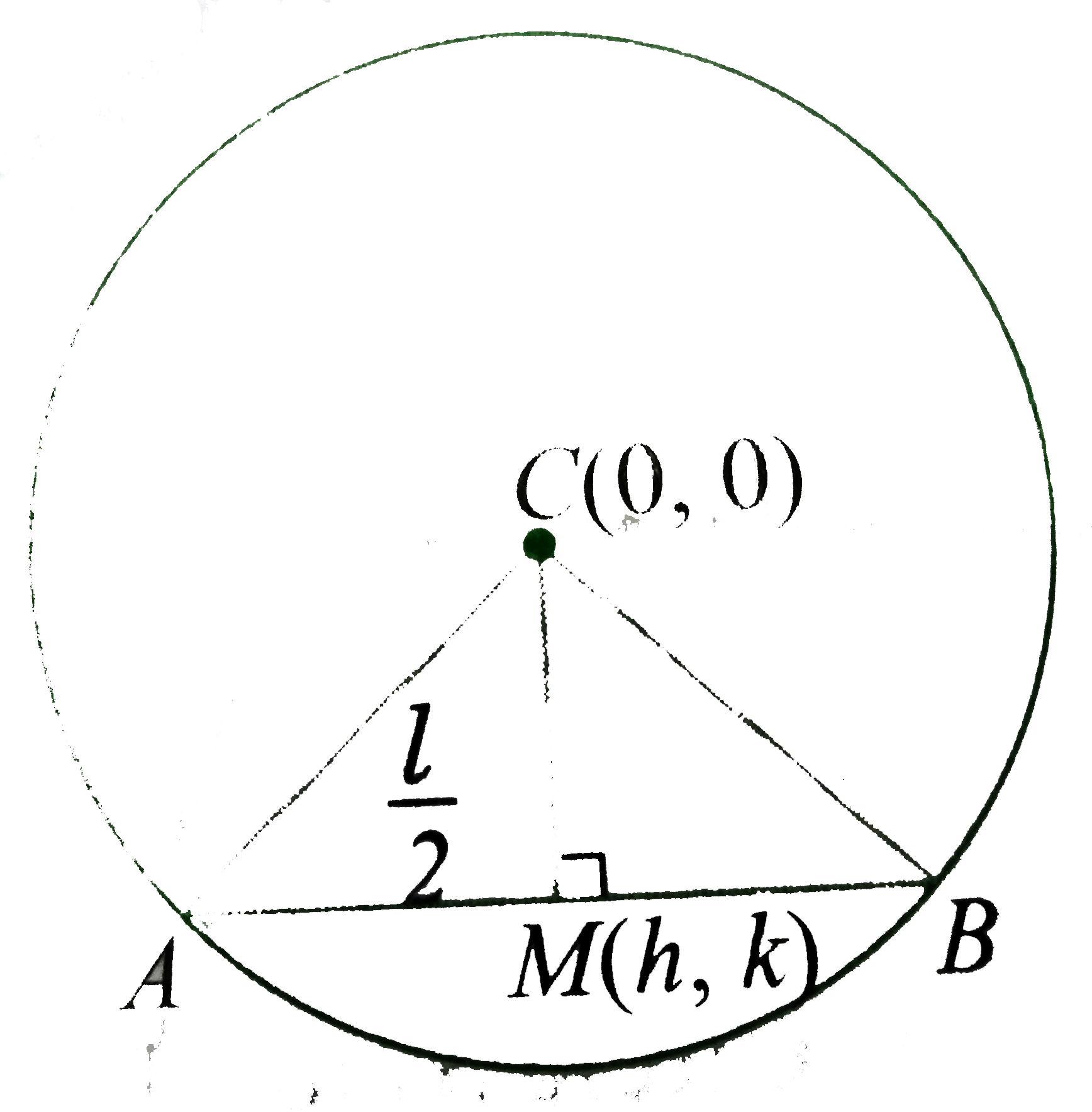
- Find the locus of the midpoint of the chords of circle x^(2)+y^(2)=a^(...
Text Solution
|
- Find the derivative of y = ln(cos x^2).
Text Solution
|
- Let x^(2)+y^(2)+2gx+2fy+c=0 be an equation of circle. Match the follow...
Text Solution
|
- Match the following lists.
Text Solution
|
- Find the derivative of y = ln(2x^3 − x)^2
Text Solution
|
- Find the derivative of y = x ln^3 x.
Text Solution
|
- Match the conics in List I with the statements// expressions in List I...
Text Solution
|