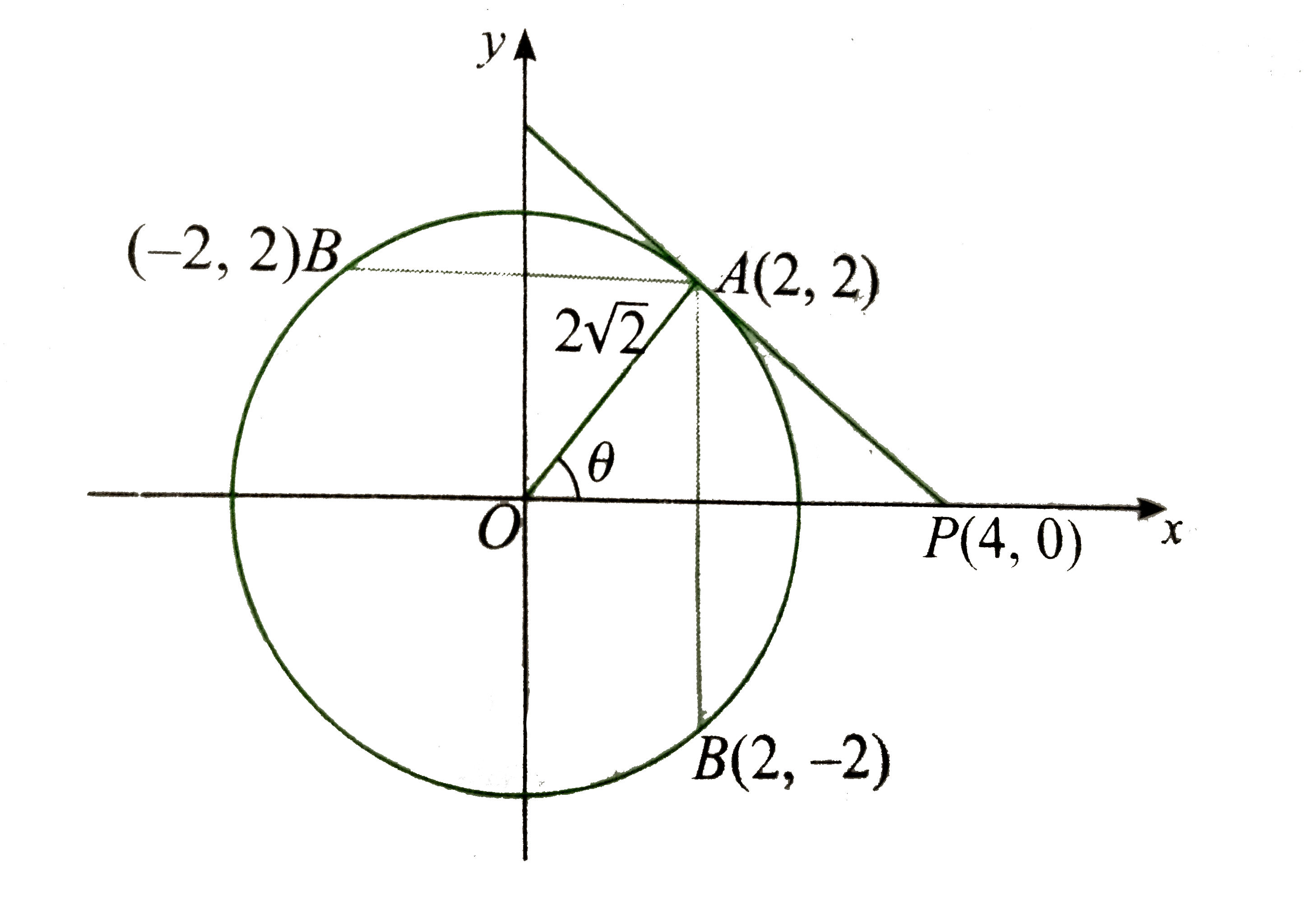Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-CIRCLE -Exercise 4.1
- If a circle whose center is (1,-3) touches the line 3x-4y-5=0 , then f...
Text Solution
|
- Find the equation of the circle which touches the x-axis and whose ...
Text Solution
|
- Find the equation of the circle which touches both the axes and the ...
Text Solution
|
- 2x+y=0 is the equation of a diameter of the circle which touches the l...
Text Solution
|
- Find the equation of the circle with center at (3,-1) and which cuts o...
Text Solution
|
- If one end of the diameter is (1, 1) and the other end lies on the lin...
Text Solution
|
- Tangent drawn from the point P(4,0) to the circle x^2+y^2=8 touches it...
Text Solution
|
- If the line x+2b y+7=0 is a diameter of the circle x^2+y^2-6x+2y=0 , t...
Text Solution
|
- Find the length of intercept, the circle x^2+y^2+10 x-6y+9=0 makes on ...
Text Solution
|
- If one end of the a diameter of the circle 2x^2+2y^2-4x-8y+2=0 is (3, ...
Text Solution
|
- Prove that the locus of the point that moves such that the sum of the ...
Text Solution
|
- Number of integral values of lambda for which x^2 + y^2 + 7x + (1-lamb...
Text Solution
|
- Prove that the locus of the centroid of the triangle whose vertices ar...
Text Solution
|
- Find the locus of center of circle of radius 2 units, if intercept cut...
Text Solution
|