Home
Class 12
MATHS
If the tangent at (3,-4) to the circle ...

If the tangent at `(3,-4)` to the circle `x^2 +y^2 -4x + 2y-5 =0` cuts the circle `x^2 +y^2+16x + 2y +10=0` in A and B then the midpoint of AB is

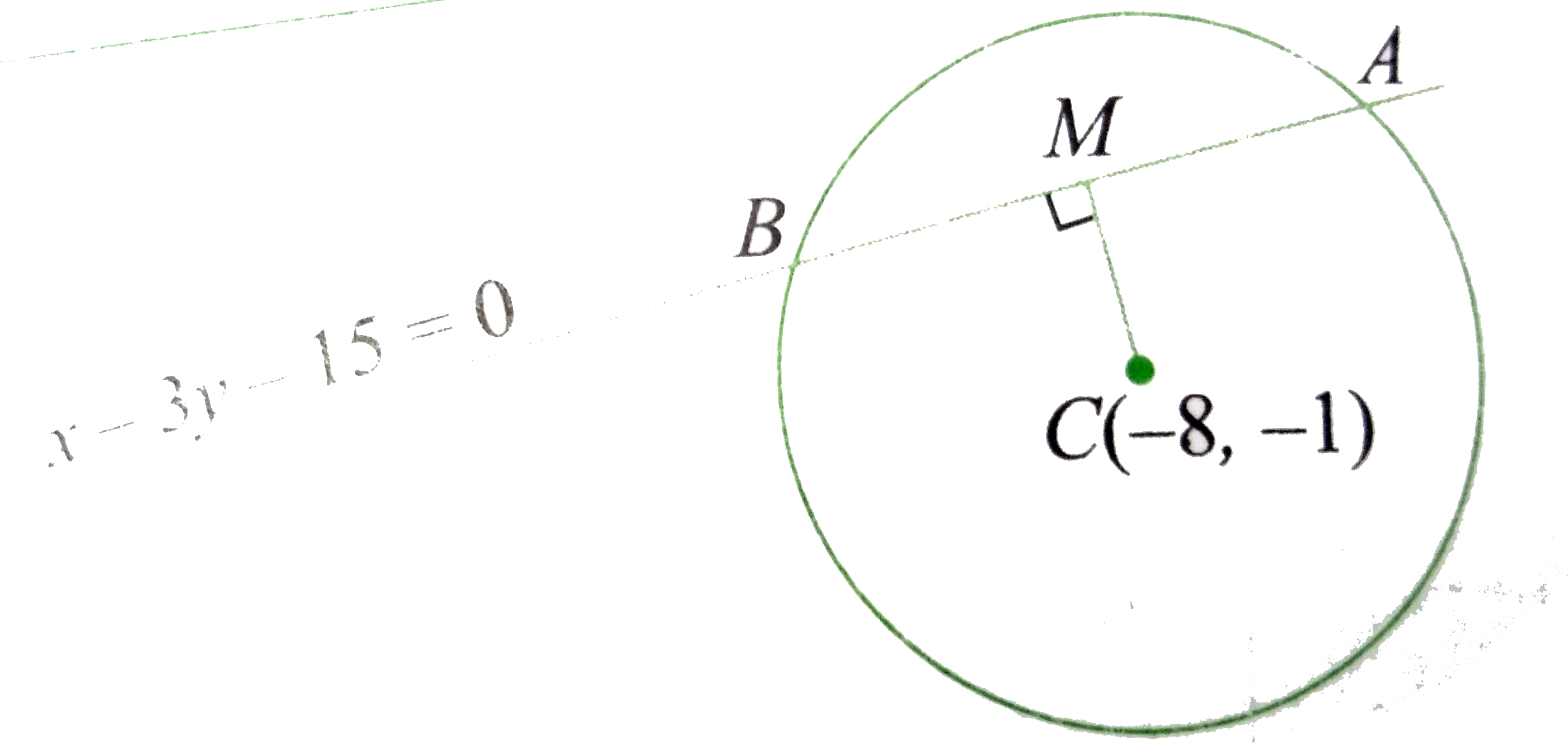
Text Solution

Verified by Experts

The correct Answer is:
`(-6,-7)`
Equation of tangent to circle `x^(2)+y^(2)-4x+2y-5=0` at point (3,-4) is
`3x-4y-2(x+3)=(y-4)-5=0`
or `x-3y-15=0` (1)

Center of the second circle is `C(-8,-1)`.
Slope of CM is `'-3'`
Equation of CM is `y+1= -3 (x+8)`
or `3x+y+25=0` (2)
Solving (1) and (2), we get `M -= (-6,-7)`
Promotional Banner

Topper's Solved these Questions

Similar Questions

Explore conceptually related problems

The circle x^2 + y^2 - 8x + 4y + 4 = 0 toches

The circle x^2 + y^2 - 3x - 4y + 2 = 0 cuts the x axis at the points

The circle x^2 + y^2 - 4x + 6y + c = 0 touches x axis if

If the tangents are drawn to the circle x^2+y^2=12 at the point where it meets the circle x^2+y^2-5x+3y-2=0, then find the point of intersection of these tangents.

If y=2x+c is tangent to the circle x^(2)+y^(2)=16 find c.

If the tangent at (1,7) to curve x^(2)=y-6 touches the circle x^(2)+y^(2)+16x+12y+c=0 then the value of c is

If y=4x+c is a tangent to the circle x^(2)+y^(2)=9 , find c.

If the line a x+b y=2 is a normal to the circle x^2+y^2-4x-4y=0 and a tangent to the circle x^2+y^2=1 , then a and b are

A circle touching the line x +y - 2 = 0 at (1,1) and cuts the circle x^(2) +y^(2) +4x +5y - 6 = 0 at P and Q. Then