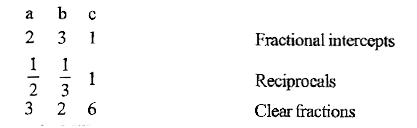Text Solution
Verified by Experts
Topper's Solved these Questions
SOLID STATE
BRILLIANT PUBLICATION|Exercise LEVEL-I|50 VideosSOLID STATE
BRILLIANT PUBLICATION|Exercise LEVEL-II|50 VideosSOLID STATE
BRILLIANT PUBLICATION|Exercise QUESTION (LEVEL -II) (Assertion-Reason)|4 VideosREDOX REACTION & ELECTROCHEMISTRY
BRILLIANT PUBLICATION|Exercise QUESTION (ELECTROCHEMISTRY) (LEVEL -II) (ASSERTION-REASON)|3 VideosSOLUTIONS
BRILLIANT PUBLICATION|Exercise Level-III (Linked Comprehension Type)|12 Videos
Similar Questions
Explore conceptually related problems
BRILLIANT PUBLICATION-SOLID STATE-QUESTION
- A compound of elements X and Y crystallizes in cubic structure where X...
Text Solution
|
- A cubic crystalline solid contains A atoms at the comers and B atoms a...
Text Solution
|
- An alloy of silver and copper crystallizes in a cubic lattice in which...
Text Solution
|
- A solid has cubic structure in which X atoms are located at the corner...
Text Solution
|
- In a solid XY, having fcc structure, X atoms occupy the comers of the ...
Text Solution
|
- Xenon crystallises in fcc structure with edge length 630 pm. Calculate...
Text Solution
|
- A metal of atomic mass 60u has a body centred cubic lattice. The edge ...
Text Solution
|
- An element of density 7.2 g cm^(-3) occurs in bcc structure with unit ...
Text Solution
|
- What is the concentration of cation vacancies if NaCl is doped with 10...
Text Solution
|
- What is the concentration of cation vacancies if KCl is doped with 0.0...
Text Solution
|
- The CsCl lattice (bcc) is more stable than NaCl(fc c). Why do halides ...
Text Solution
|
- In a cubic lattice, the close packed structure of mixed oxides of the ...
Text Solution
|
- Calculate the miller indices of crystal planes which cut through the c...
Text Solution
|
- Calculate the distance between 200, 110 and 222 planes of a body centr...
Text Solution
|