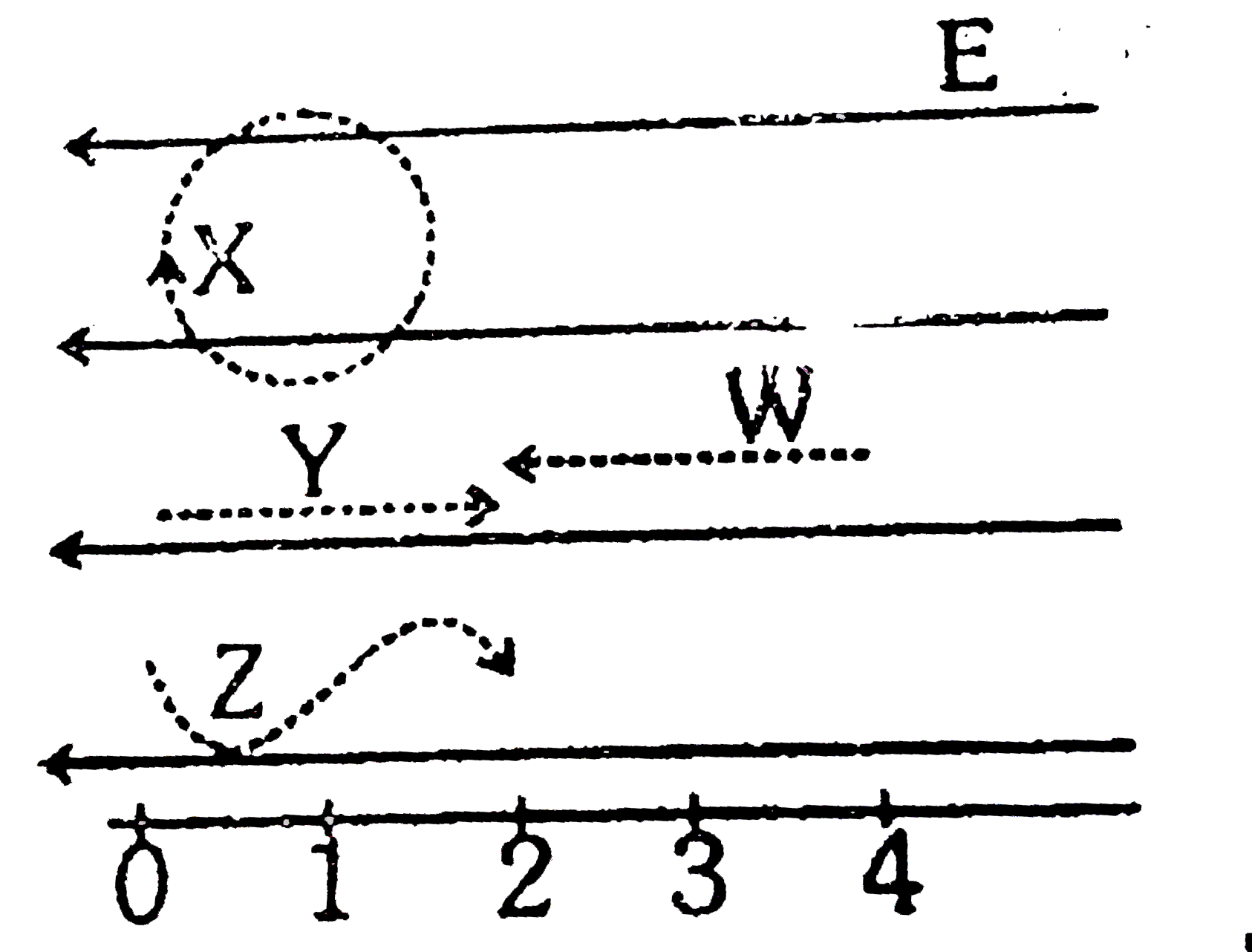Home
Class 11
PHYSICS
In the diagram (given below), the broken...

In the diagram (given below), the broken lines represent the paths followed by particles W, X, Y and Z respectively through the contant field E. The number below the field represent meters.

Suppose that the field strength E is `10 N//C` and particle Y has a charge of `-10 C`. When is the mass of particle Y

A

1 kg

B

2 kg

C

3 kg

D

4 kg

Text Solution

Verified by Experts

The correct Answer is:
D
`a=(qE)/(m)` & `v^(2)=u^(2)+2as`
Promotional Banner

Topper's Solved these Questions

  • MISCELLANEOUS

    ALLEN |Exercise Comprehension 9|2 Videos

  • MISCELLANEOUS

    ALLEN |Exercise Exersice-04[A]|34 Videos

  • MISCELLANEOUS

    ALLEN |Exercise Comprehension 7|3 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN |Exercise BEGINNER S BOX-7|8 Videos

  • PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT

    ALLEN |Exercise EXERCISE-IV|7 Videos

Similar Questions

Explore conceptually related problems

In the diagram (given below), the broken lines represent the paths followed by particles W, X, Y and Z respectively through the contant field E. The number below the field represent meters. Suppose particle Z has a charge of +2C , and is begins and end at rest. If E is 5N//C , how much work is done on particle Z

In the diagram (given below), the broken lines represent the paths followed by particles W, X, Y and Z respectively through the contant field E. The number below the field represent meters. If the particles are positively charged, which particles increased their electric potential energy constant, none of the particle increased their electric potential energy

A particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed v_x (like particle 1 in figure. The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL^(2)//(2m v_(x)^(2)) . Compare this motion with motion of a projectile in gravitational field discussed in Section 4.10 of Class XI Textbook of Physics.

(a) Magnetic field lines show the direction (at every point) along which a small magnetised needle aligns at the point). Do the magnetic field lines also represent the lines of force on a moving charged particle at every point? (b) Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid. Why? (c) If magnetic monopoles existed, how would the Gauss's law of magnetism be modified? (d) Does a bar magnet exert a torque on itsell due to its own field? Does one element of a current-carrying wire exert a force on another element of the same wtre? (e) Magnetic field arises due to charges in motion. Can a system have magnetic moments even though its net charge is zero?

A magnetic field set up using Helmholtz coils (described in Exercise 4.16) is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0xx10^(-5)Vm^(-1) , make a simple guess as to what the beam contains. Why is the answer not unique ?

When a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100sqrt(2) m//s , at an angle of 45^(@) with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10 m//s^(2) . Consider an observer in frame D (of the previous question), who observes a body of mass 10 kg acelerating in the upward direction at 30 m//s^(2) (w.r.t. himself). The net force acting on this body, as observed from the ground is :-

When a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100sqrt(2) m//s , at an angle of 45^(@) with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10 m//s^(2) . " A third observer (C) close to the surface of the reports that particle is initially travelling at a speed of 100sqrt(2) m//s making on angle of 45^(@) with the horizontal, but its horizontal motion is northward". The third observer is moving in :-

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. The limiting electric potential of the sphere is