Home
Class 11
PHYSICS
A cavity pf radius r is present inside a...

A cavity pf radius `r` is present inside a solid dielectric sphere of radius ` R`, having a volume charge density of ` rho`. The distance between the centres of the sphere and the cavity is a . An electron `e` is kept inside the cavity at an angle ` theta = 45^@` as shown . how long will it take to touch the sphere again ?
.

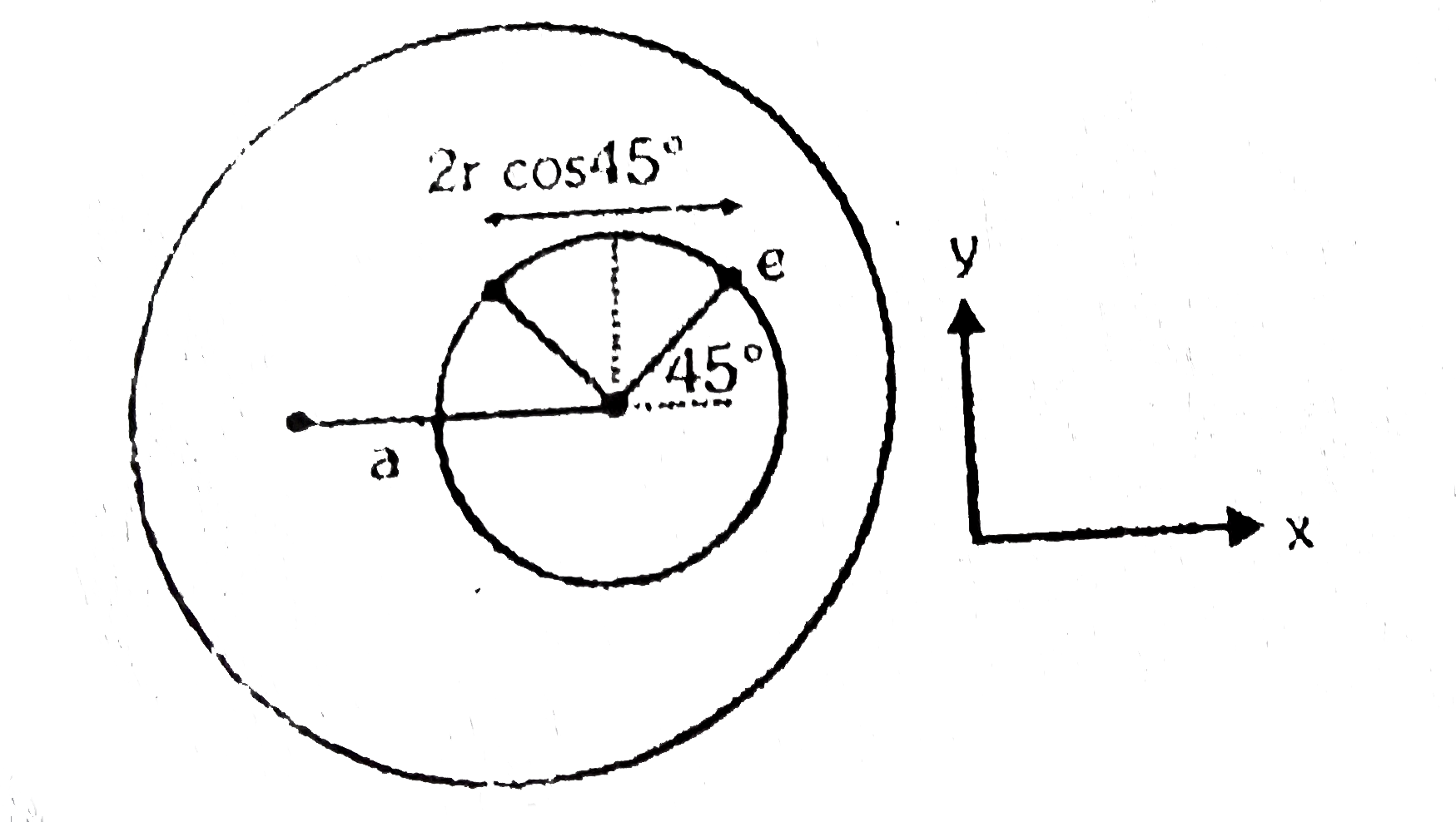
Text Solution

Verified by Experts

The correct Answer is:
`sqrt((6sqrt(2)mr in_(0))/(e rho a))`
The direction of electric field inside the cavity in -ve x direction and of constant magnitude `(rho a)/(3 in_(0))`

For touch the sphere again, electron must move `2r cos 45^(@)` (as shown) distance
`:. 1/2 [(rho a)/(3 in_(0))xxe/m]xxt^(2)=sqrt(2)r :. t=sqrt((6sqrt(2)mr in_(0))/(e rho a))`
Promotional Banner

Topper's Solved these Questions

  • MISCELLANEOUS

    ALLEN |Exercise Exercise-05(A)|35 Videos

  • MISCELLANEOUS

    ALLEN |Exercise Exercise-05(B)|19 Videos

  • MISCELLANEOUS

    ALLEN |Exercise Exersice-04[A]|34 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN |Exercise BEGINNER S BOX-7|8 Videos

  • PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT

    ALLEN |Exercise EXERCISE-IV|7 Videos

Similar Questions

Explore conceptually related problems

A cavity of radius R//2 is made inside a solid sphere of radius R . The centre of the cavity is located at a distance R//2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R//2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM//R^(2) , where M is the mass of the solide sphere]

A hollow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre

Let P(r)=(Q)/(piR^4)r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r_1 from the centre of the sphere, the magnitude of electric field is:

A sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:

A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre

Q amount of electric charge is present on the surface of a sphere having radius R. Calculate the total energy of the system.

The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density rho=A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:

The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), has volume charge density rho =A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant is :

Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities rho_1 and rho_2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio rho_1/rho_2 can be

A metallic spherical shell has an inner radius R j and outer radius R_2 . A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?