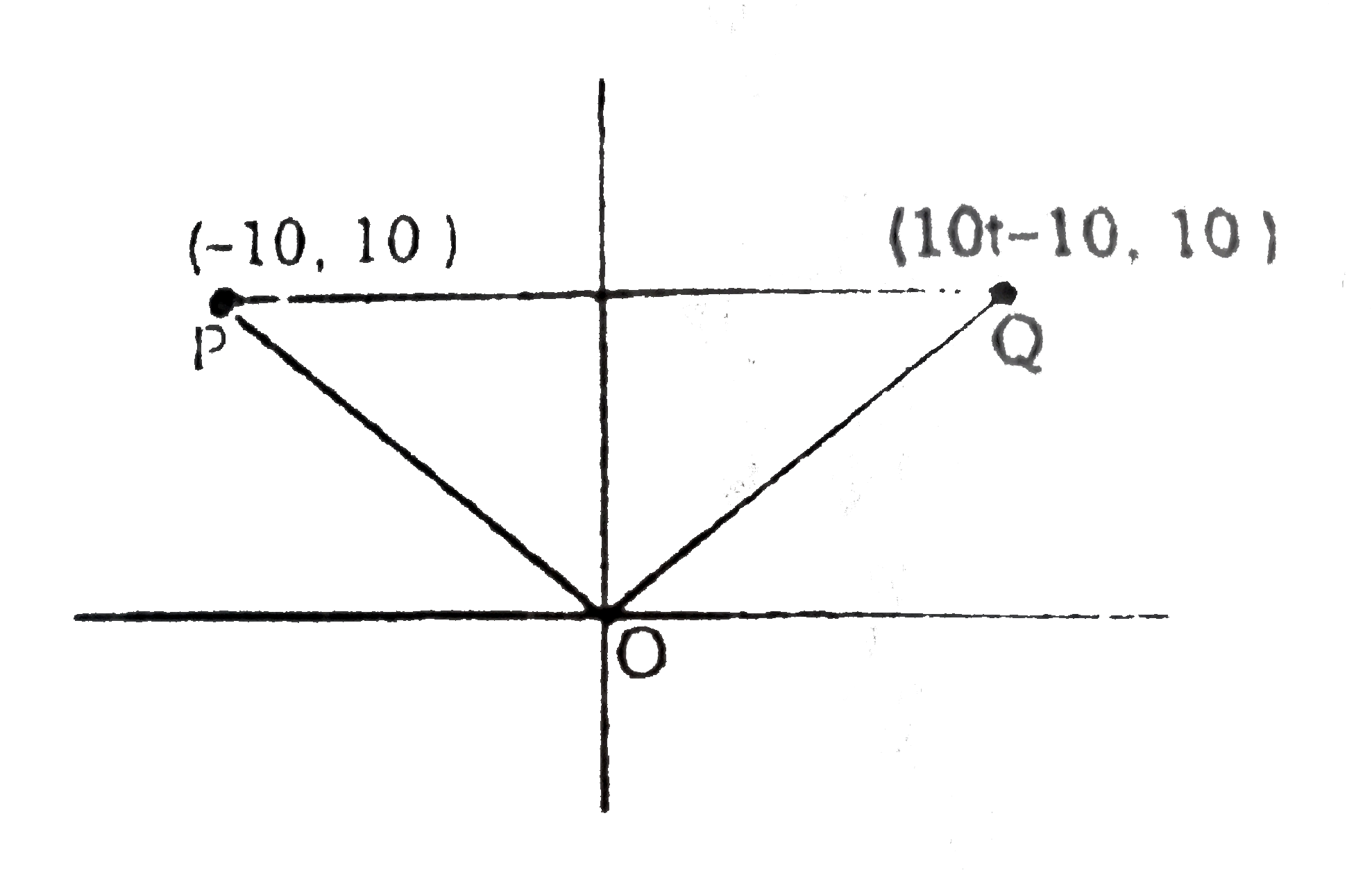
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
KINEMATICS
ALLEN |Exercise Exercise-05 [A]|11 VideosKINEMATICS
ALLEN |Exercise Exercise-05[B]|5 VideosKINEMATICS
ALLEN |Exercise EXERCISE-04[A]|35 VideosERROR AND MEASUREMENT
ALLEN |Exercise Part-2(Exercise-2)(B)|22 VideosKINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN |Exercise BEGINNER S BOX-7|8 Videos
Similar Questions
Explore conceptually related problems
ALLEN -KINEMATICS-Exercise-04[B]
- Two towns A and B are connected by a regular bus service with a bus le...
Text Solution
|
- The brakes of a train which is travelling at 30 m//s are applied as th...
Text Solution
|
- A ship is moving at a constant speed of 10 km//hr in the direction of ...
Text Solution
|
- A balloon starts ascending from the ground at a constant speed of 25 m...
Text Solution
|
- Two bodies move in a straight line towards each other at initial veloc...
Text Solution
|
- A helicopter takes off along the vertical with an acceleration a = 3m/...
Text Solution
|
- Two swimmers start a race. One who reaches the point C first on the ot...
Text Solution
|
- A swimmer starts to swim from point a to cross a river. He wants to re...
Text Solution
|
- Hailstones falling vertically with speed of 10 m/s hit with respect to...
Text Solution
|
- A shell is fired from a point O at an angle of 60^(@) with a speed of ...
Text Solution
|
- Two inclined planes OA and OB having inclinations 30^(@) and 60^(@) re...
Text Solution
|
- A stone is projected from the ground in such a direction so as to hit ...
Text Solution
|
- A projectile is launched at an angle alpha from a cliff of height H ab...
Text Solution
|
- A particle is projected with velocity 2(sqrt(gh)), so that it just cle...
Text Solution
|