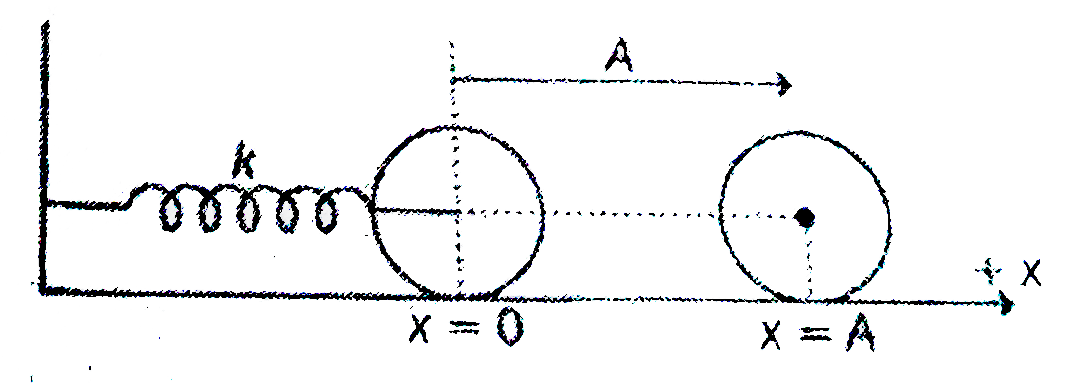Home
Class 12
PHYSICS
In the problem if k = 10 N/m, m=2kg, R=1...

In the problem if k = 10 N/m, m=2kg, R=1m and A=2m. Find linear speed of the disc at mean position.

A

`sqrt((40)/(3)) m//s`

B

`sqrt(20) m//s`

C

`sqrt((10)/(3)) m//s`

D

`sqrt((50)/(3)) m//s`

Text Solution

Verified by Experts

The correct Answer is:
A
`1/(2)kAY^(2) = 1/2 mv^(2) (1+(k^(2))/(R^(2))) = 1/2mv^(2)(1+1/2) = 3/4 mv^(2)`
`v = sqrt((2kA^(2))/(3m)) = sqrt((2(10)(2)^(2))/(3(2))) = sqrt((40)/(3))ms^(-1)`
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Comprehension Base Questions (3)|2 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Comprehension Base Questions (4)|2 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Comprehension Base Questions (1)|2 Videos

  • RACE

    ALLEN |Exercise Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)|25 Videos

  • TEST PAPER

    ALLEN |Exercise PHYSICS|4 Videos

Similar Questions

Explore conceptually related problems

A bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation. The speed of the bob at its mean position is 1 m s^(-1) . What is the trajectory of the bob if the string is cut when the bob is (a) at one of its extreme positions, (b) at its mean position.

A bird moves from point (1 m, -2 m, 3 m) to (4 m, 2 m, 3 m) . If the speed of the bird is 10 m//s , then the velocity vector of the bird in m//s is:

A particle executing a linear SHM has velocities of 8 m/s, 7 m/s and 4 m/s, respectively at three points at distances of x m, (x+1) m and (x+2)m from the mean position. What is the maximum velocity of the particle ?

Infinite particles each of mass 'M' are placed at positions x=1 m, x=2m, x=4 m .... prop . Find the gravitational field intensity at the origin.

Tow men of masses m_(1)and m_(2) hold on the opposite ends of a rope passing over a frictionless pulley. The men m_(1) climbs up the pore with an acceleration of 1.2m//s^(2) relative to the rope. The mann m_(2) climbs up the rope with an acceleration of 2m//s^(2) relative to the rope. Find the tension in the rope if m_(1)40 kg and m_(2)=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.

The particles of mass m_(1),m_(2) and m_(3) are placed on the vertices of an equilateral triangle of sides .a.. Find the centre of mass of this system with respect to the position of particle of mass m_(1) .

The equation for the speed of sound in a gas states that v=sqrt(gammak_(B)T//m) . Where,Speed v is measured in m/s, gamma is a dimensionless constant, T is temperature in kelvin (K), and m is mass in kg. Find the SI units for the Boltzmann constant, k_(B) ?

A block of mass m= 1 kg , moving on a horizontal surface with speed v_(t)= 2 ms^(-1) enters a rough patch ranging from x= 0.10m" to "x= 2.01m . The retarding force F_(r ) on the block in this range is inversely proportional to x over this range, F_(r )= (-k)/(x)" for "0.1 lt x lt 2.01m = 0 " for "x lt 0.1m" and "x gt 2.01m where k= 0.5 J . What is the final kinetic energy and speed v_(f) of the block as it crosses this patch?

A cylindrical block of length 0.4 m and area of cross-section 0.04 m^2 is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K . if the thermal conductivity of the material of the cylinder is 10 "watt"// m.K and the specific heat of the material of the disc is 600J//kg.K , how long will it take for the temperature of the disc to increase to 350 K ? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder.