Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -TEST PAPER-CHEMISTRY SECTION-II
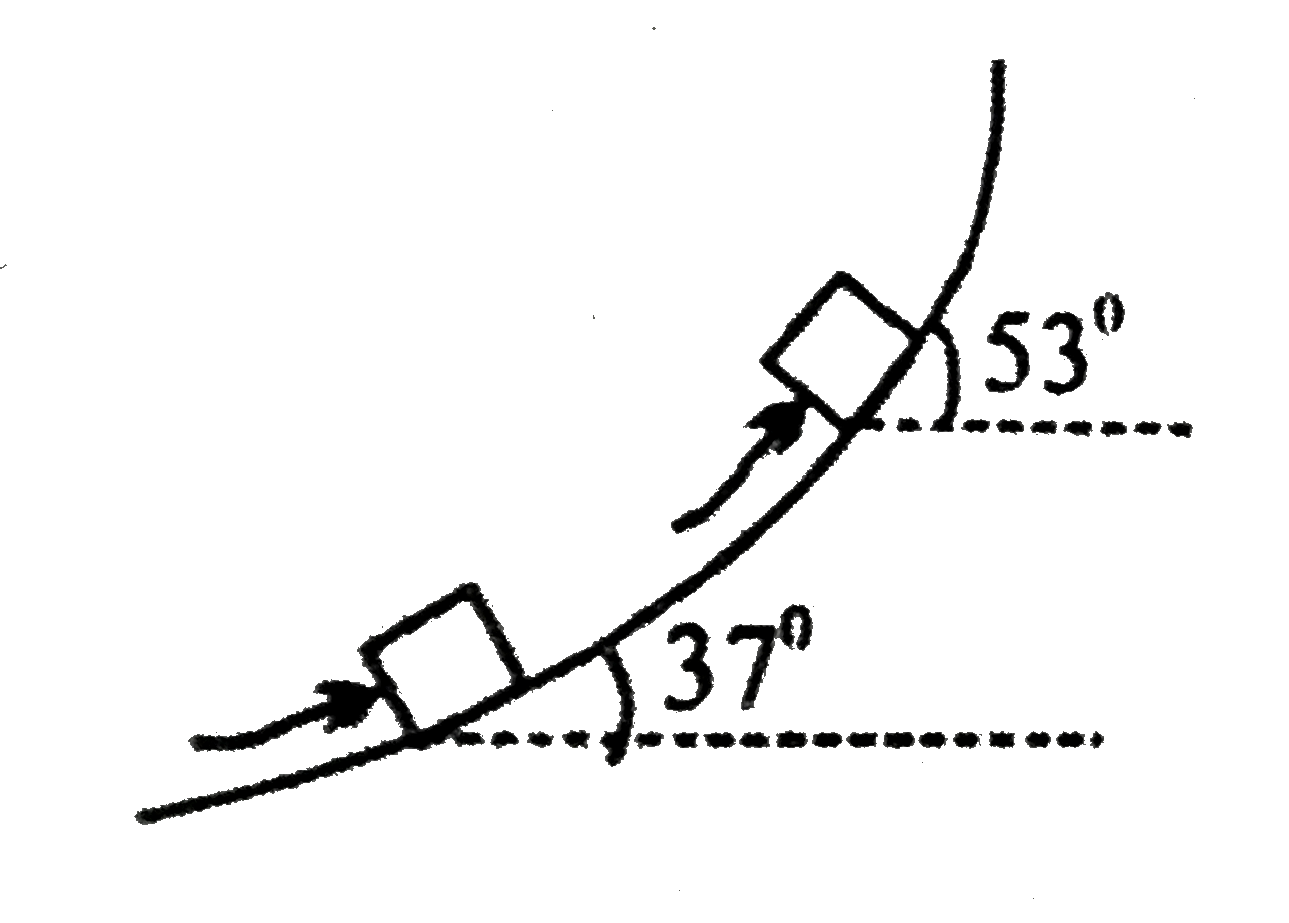
- A man can just push a box on 37^(@) concreate slope. When he keeps it ...
Text Solution
|
- The molar mass of a substance , each molecule of which contains 9 C at...
Text Solution
|
- 1 mole of a molecular species X2^(-2) has 40 moles neutrons & 36 moles...
Text Solution
|
- Find the difference of percentage ionic character in N-F & B-F bond by...
Text Solution
|
- Find the values of 'a' in equation 'a+0.65 (n+1) which gives value of ...
Text Solution
|
- Find the maximum number of electron in Chromium which is present in ax...
Text Solution
|
- The number of lone pair in C3N3Cl3 is
Text Solution
|
- Find the number of ion(s) having radius greater then Li^+. Rb^+, Ba^...
Text Solution
|
- Find the total number of lone pair in poly phosphoric acid having four...
Text Solution
|
- Two balls of mass m1 and m2 (m1 gt m2) are thrown from the same point ...
Text Solution
|
- A particle is moving along x-axis. Velocity of particle changes as v=s...
Text Solution
|
- Which of the following order is CORRECT according to given property ?
Text Solution
|
- Which of the following set of quantum numbers will have lowest energy ...
Text Solution
|
- Which of the following species have partially filled d-subshell ?
Text Solution
|
- Which of the following set is pair of isoster species.
Text Solution
|
- Which of the following statement is CORRECT ?
Text Solution
|
- Maximum number of +1/2 spin electrons in Cr which have |l x m| =2
Text Solution
|