A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -BASIC MATHS-ASSERTION-REASON
- if|vecAxxvecB|=|vecA.vecB|, then angle between vecA and vecB will be
Text Solution
|
- A unit radial vector vecr makes agles of a=30^(@) relative to the x-ax...
Text Solution
|
- If hati,hatj and hatk represent unit vectors along the x,y and z-axes ...
Text Solution
|
- Find the torque (vectau=vecrxxvecF) of a force vecF=-3hati+hatj+3hatk ...
Text Solution
|
- Six vector vec(a) through vec(f) have the magnitudes and direction ind...
Text Solution
|
- If vectors vecA and vecB are such that |vecA+vecB|= |vecA|= |vecB| the...
Text Solution
|
- The equation of a curve is given as y=x^(2)+2-3x. The curve intersec...
Text Solution
|
- The sum of the series 1+(1)/(4)+(1)/(16)+(1)/(64)+....oo is
Text Solution
|
- As theta increases from 0^(@) to 90^(@), the value of cos theta is
Text Solution
|
- The coordinates of a particle moving in XY-plane very with time as x=4...
Text Solution
|
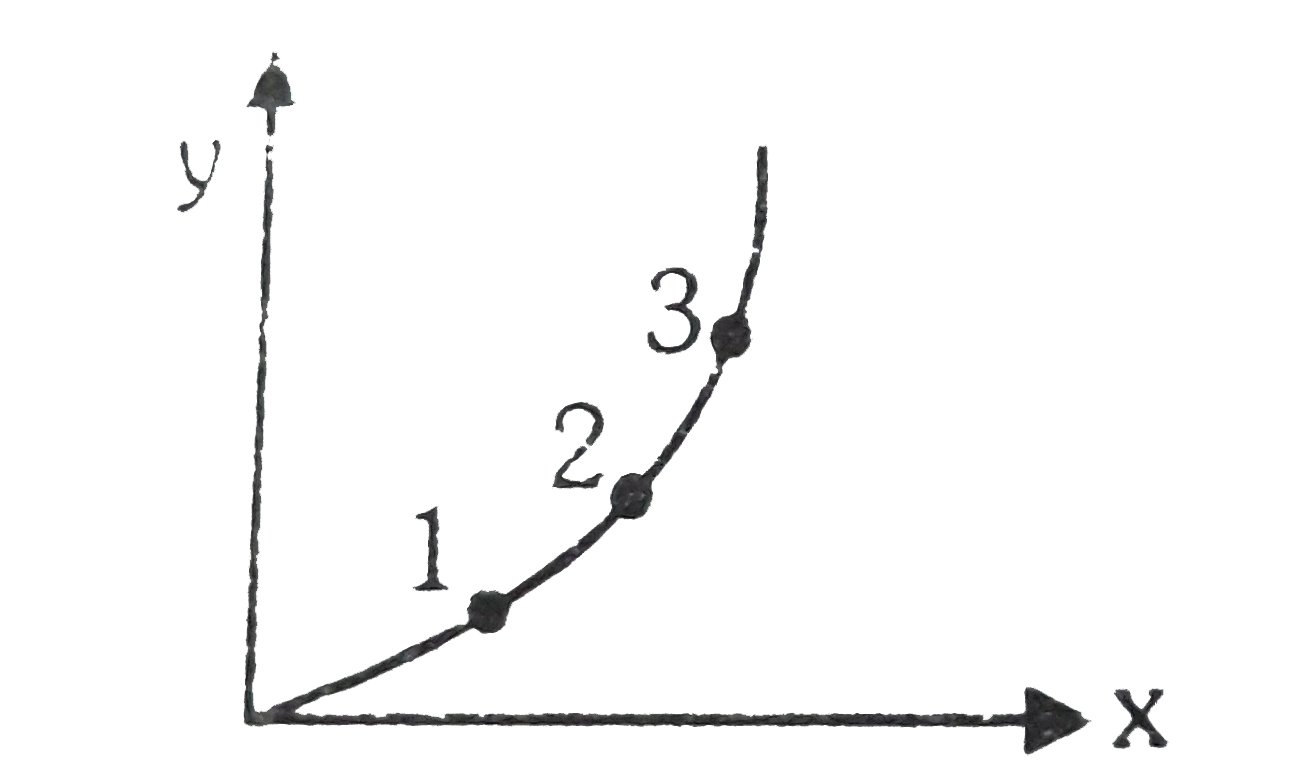
- The slope of graph as shown in figure at points 1,2 and 3 is m(1), m(2...
Text Solution
|