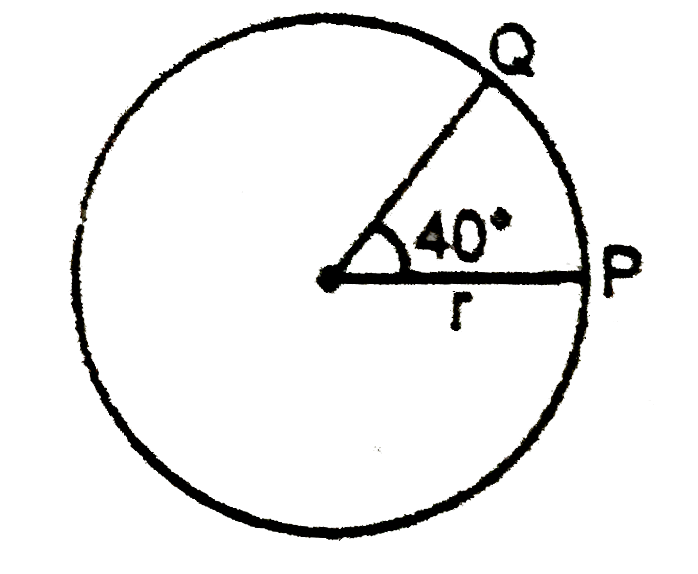Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -MOTION IN A PALNE-Comprehension#5
- A body is projected vertically upwards with speed u from the top of a ...
Text Solution
|
- Engine of a train that is moving with unifrom acceleration passes a po...
Text Solution
|
- An object is projected upwards with a velocity of 100m//s. It will str...
Text Solution
|
- A particle is moving in a circle of radius r with speed v as shown in ...
Text Solution
|
- A stone falls from a ballon that id descending at a uniform rate of 12...
Text Solution
|
- A man walks for some time 't' with velocity(v) due east. Then he walks...
Text Solution
|