Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN |Exercise BEGINNER S BOX-1|6 VideosKINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN |Exercise BEGINNER S BOX-2|7 VideosKINEMATICS
ALLEN |Exercise EXERCISE-2|89 VideosMISCELLANEOUS
ALLEN |Exercise Question|1 Videos
Similar Questions
Explore conceptually related problems
ALLEN -KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)-BEGINNER S BOX-7
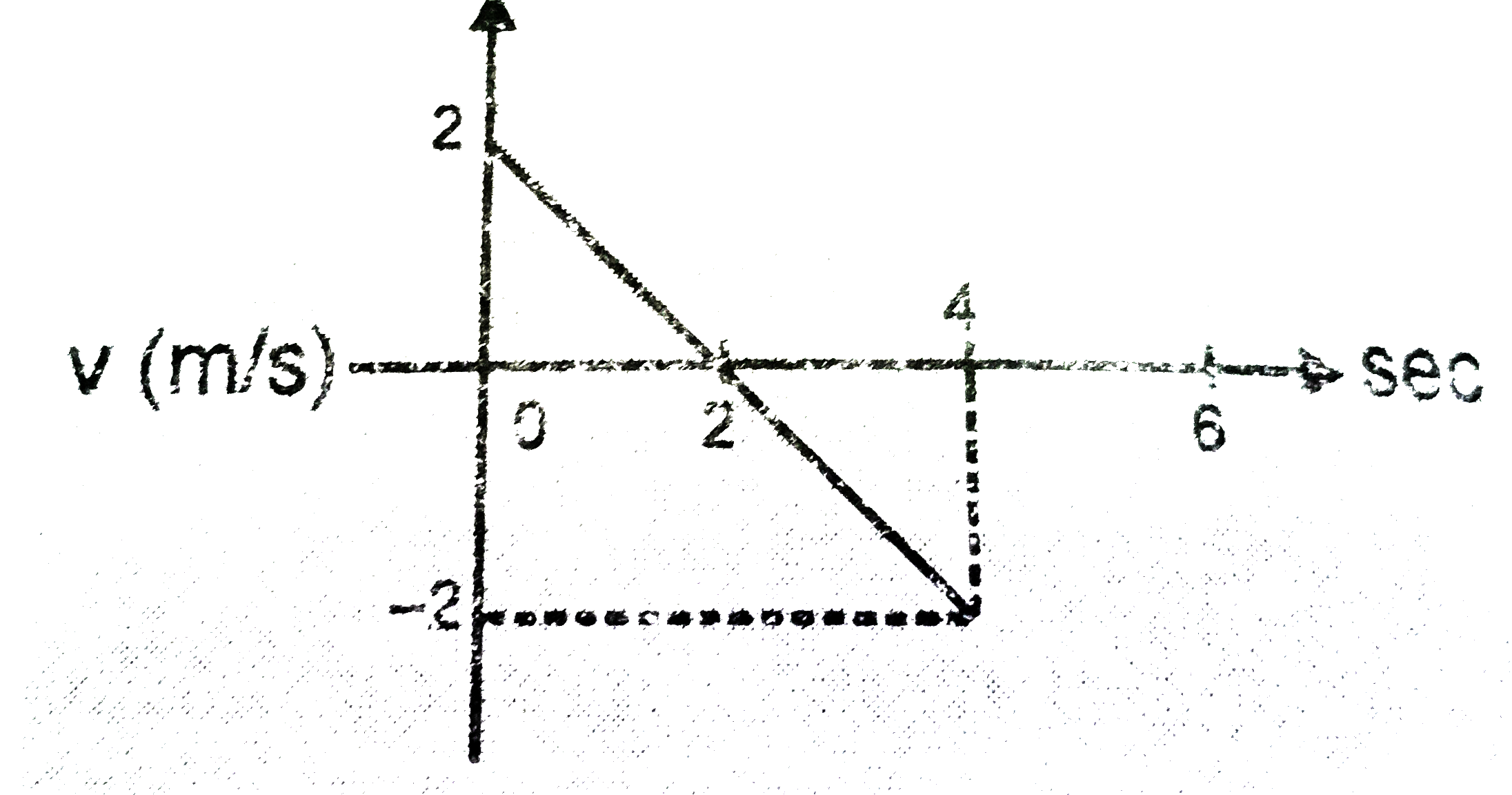
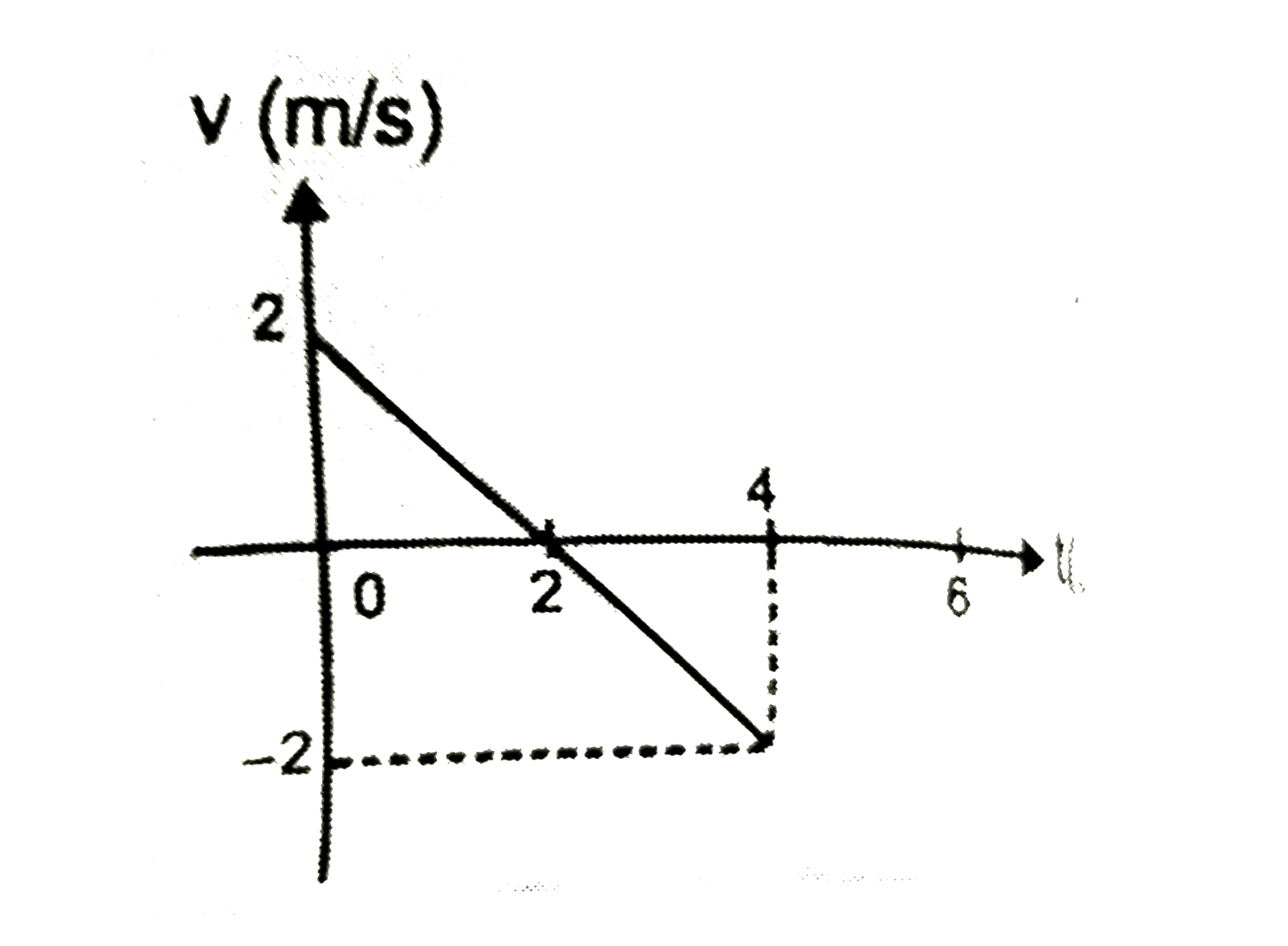
- Velocity time graph for a particle moving in a line is given. Calcul...
Text Solution
|
- A football player kicks a ball at an angle of 30^(@) with an initial s...
Text Solution
|
- A cricketer can throw a ball to a maximum horizontal distance of 100 ...
Text Solution
|
- Two bodies are thrown with the same initial speed at angles alpha and ...
Text Solution
|
- A ball is thrown at angle theta and another ball is thrown at angle (9...
Text Solution
|
- The range of a particle when lauched at an angle of 15^(@) with the ho...
Text Solution
|
- Show that projection angle theta(0) for a projectile launched from the...
Text Solution
|
- A ball of mass m is thrown vertically up. Another of mass 2m is thrown...
Text Solution
|
- The ceiling of a long hall is 20 m high. What is the maximum horizonta...
Text Solution
|