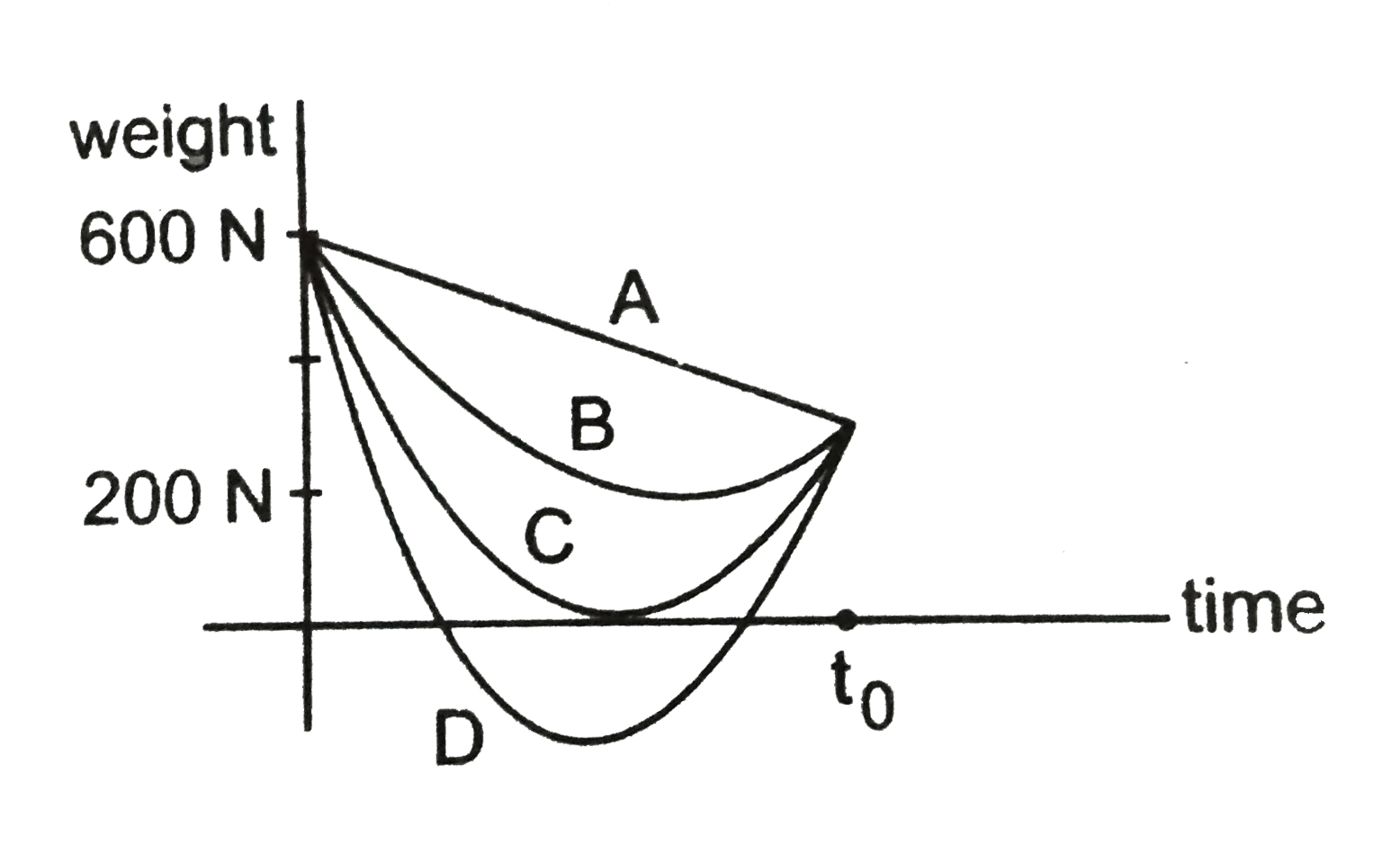
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -GRAVITATION-EXERCISE 1
- A satellite of the earth is revolving in a circular orbit with a unifo...
Text Solution
|
- Following curve shows the variation of intesity of gravitational field...
Text Solution
|
- Suppose the acceleration due to gravity at earth's surface is 10ms^-2 ...
Text Solution
|
- Assume that a tunnel is dug through earth from North pole to south pol...
Text Solution
|
- Mars has a diameter of approximately 0.5 of that of earth, and mass of...
Text Solution
|
- Three equal masses of 1 kg each are placed at the vertices of an equil...
Text Solution
|
- One can easily "weigh the earth" by calculating the mass of earth usin...
Text Solution
|
- Acceleration due to gravity at the centre of the earth is :-
Text Solution
|
- The value of 'g' on earth surface depends :-
Text Solution
|
- The value of 'g' reduces to half of its value at surface of earth at a...
Text Solution
|
- The acceleration due to gravity on a planet is 1.96 ms^(-1). If it is ...
Text Solution
|
- If the earth stops rotating sudenly, the value of g at a place other t...
Text Solution
|
- Diameter and mass of a planet is double that earth. Then time period o...
Text Solution
|
- Gravitation on moon is (1)/(6) th of that on earth. When a balloon fil...
Text Solution
|
- The acceleration due to gravity g and mean density of earth rho are re...
Text Solution
|
- Will 1 kg sugar be more at poles or at the equator?
Text Solution
|
- When you move from equator to pole, the value of acceleration due to g...
Text Solution
|
- When the radius of earth is reduced by 1% without changing the mass, t...
Text Solution
|
- Weight of a body of mass m decreases by 1% when it is raised to height...
Text Solution
|
- Acceleration due to gravity at earth's surface if 'g' m//s^(2). Find t...
Text Solution
|