Home
Class 12
MATHS
Let P(x) denote the probability of the o...

Let `P(x)` denote the probability of the occurrence of event `xdot` Plot all those point `(x , y)=(P(A),P(B))` in a plane which satisfies the conditions, `P(AuuB)geq3//4a n d1//8lt=P(AnnB)lt=3//8`

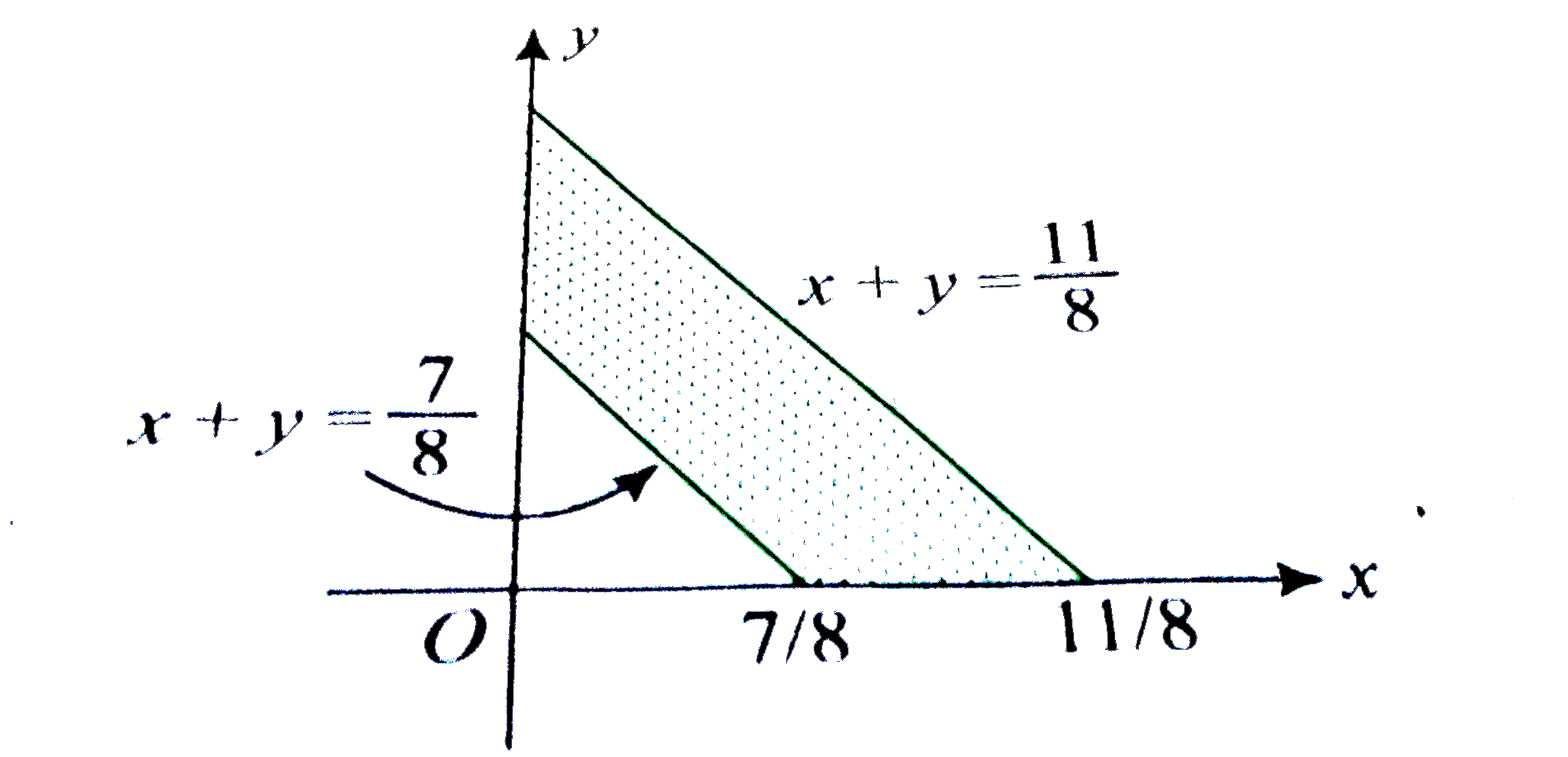
Text Solution

Verified by Experts

`P(A uu B) ge (3)/(4) and (1)/(8) le P(A nn B) le (3)/(8)`
Hence,
`P(A) + P(B) - P(A nn B) le (3)/(4)`
implies `P(A) + P(B) ge (3)/(4) + P(A nn B) ge (3)/(4) + (1)/(8) = (7)/(8)`
`implies x + y ge (7)/(8)`
We know that
`P(A nn B) le 1`
`implies P(A) + P(B) le 1 + P(A nn B) le 1 + (3)/(8) = (11)/(8)`
`implies x + y le (11)/(8)`

The shaded part in the figure is the required region.
Promotional Banner

Topper's Solved these Questions

  • PROBABILITY I

    CENGAGE PUBLICATION|Exercise Exercise 9.1|6 Videos

  • PROBABILITY I

    CENGAGE PUBLICATION|Exercise Exercise 9.2|19 Videos

  • PROBABILITY I

    CENGAGE PUBLICATION|Exercise JEE Advanced|7 Videos

  • PROBABILITY

    CENGAGE PUBLICATION|Exercise All Questions|470 Videos

  • PROBABILITY II

    CENGAGE PUBLICATION|Exercise MULTIPLE CORRECT ANSWER TYPE|6 Videos

Similar Questions

Explore conceptually related problems

If A, B are two events such that P(A cup B) ge 3/4 "and" 1/8 le P(A cap B) le 3/8

The probability of occurrence of at least one event of two events X and Y is 0.6.-If the probability of occurrence both is 0.2, find P(barX) + P(barY)

Let X denote the number of times heads occur in n tosses of a fair coin. If P(X=4),\ P(X=5)\ a n d\ P(X=6) are in AP; the value of n is

Let A and B be two independent events. The probability of their simultaneous occurrence is 1/8 and the probability that neither occurs is 3/8. Find P(A)a n dP(B)dot

Plot the region of the points P (x,y) satisfying |x|+|y| lt 1.

Let E and F be two independent events. The probability that exactly one of them occurs is 11/25 and the probability if none of them occurring is 2/25 . If P(T) denotes the probability of occurrence of the event T , then (a) P(E)=4/5,P(F)=3/5 (b) P(E)=1/5,P(F)=2/5 (c) P(E)=2/5,P(F)=1/5 (d) P(E)=3/5,P(F)=4/5

If P_(n) denotes the product of all the coefficients of (1+x)^(n) and 9!P_(n+1)=10^(9)P_(n) then n is equal to

If p be occurrence of an event in a single trail, then show that the probability of at least one occurrence in n trials is 1-(1-p)^n .

Let 0ltP(A)lt1, 0ltP(B)lt1 and P(AcupB)=P(A)+P(B)-P(A)P(B), then,

Let P(n) denote the statement that n^2+n is odd. It is seen that P(n) implies P(n+1) , P(n) is true for all