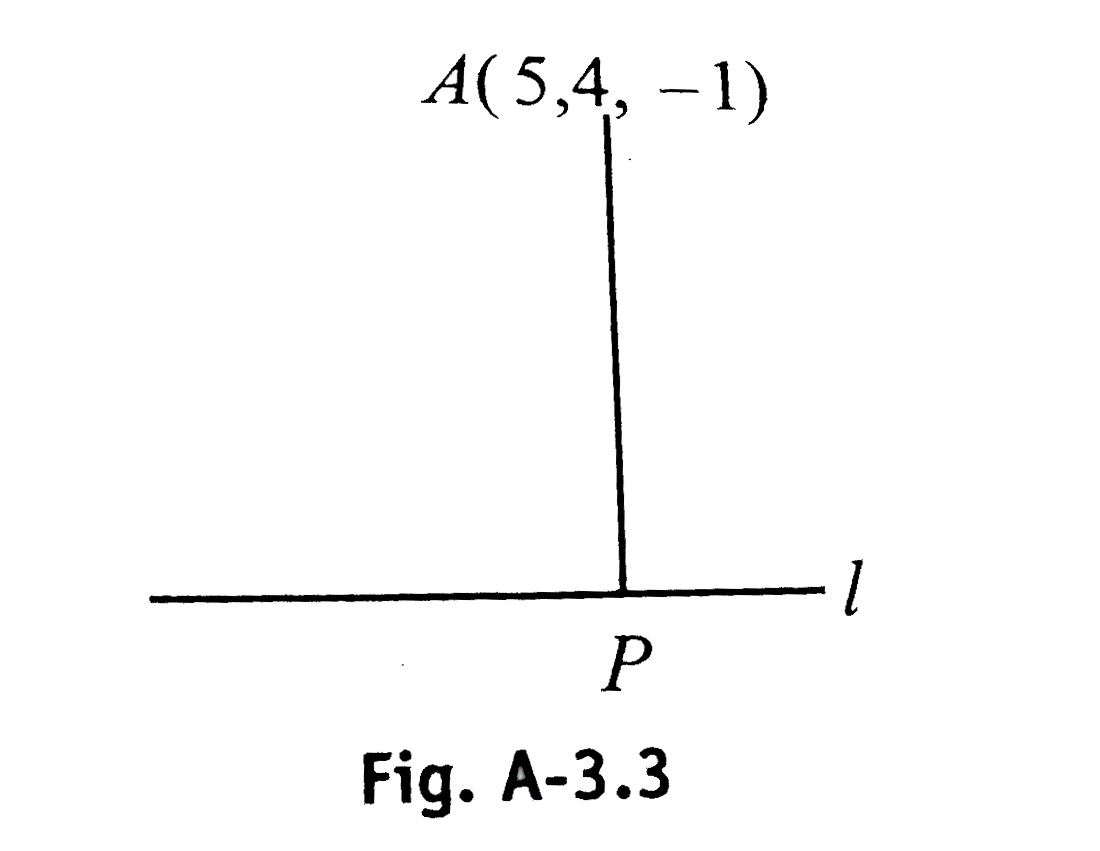Text Solution
Verified by Experts
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 3.3|19 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 3.4|5 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 3.1|12 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise All Questions|291 VideosTRIGONOMETRIC EQUATIONS
CENGAGE PUBLICATION|Exercise Archives (Numerical value type)|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-THREE-DIMENSIONAL GEOMETRY -CONCEPT APPLICATION EXERCISE 3.2
- Find the point where line which passes through point (1,2,3) and is...
Text Solution
|
- Find the equation of the line passing through the points (1,2,3)a n...
Text Solution
|
- Find the vector equation of the line passing through the point (2,-...
Text Solution
|
- Find the equation of the line passing through the point (-1,2,3) an...
Text Solution
|
- Find the equation of the line passing through the intersection (-1,3...
Text Solution
|
- The straight line (x-3)/3=(y-2)/1=(z-1)/0 is Parallel to x-axis Parall...
Text Solution
|
- Find the angle between the lines 2x=3y=-z and 6x=-y=-4z
Text Solution
|
- If the lines (x-1)/(-3)=(y-2)/(2k)=(z-3)/(-2) and (x-1)/(3k)=(y-5)/1=(...
Text Solution
|
- The equations of motion of a rocket are x=2t ,y=-4ta n dz=4t , wher...
Text Solution
|
- Find the length of the perpendicular drawn from the point(5,4,-1) t...
Text Solution
|
- Find the image of point (1,2,3) in the line (x-6)/3=(y-7)/2=(z-7)/(-2)...
Text Solution
|
- Find the shortest distance between the lines vec r=(1-lambda) hat i...
Text Solution
|
- Find the shortest distance between the z-axis and the line, x+y+2z-...
Text Solution
|
- If the lines (x-1)/2=(y+1)/3=(z-1)/4a n d(x-3)/1=(y-k)/2=z/1 intersect...
Text Solution
|
- Let l1a n dl2 be the two skew lines. If P ,Q are two distinct points o...
Text Solution
|