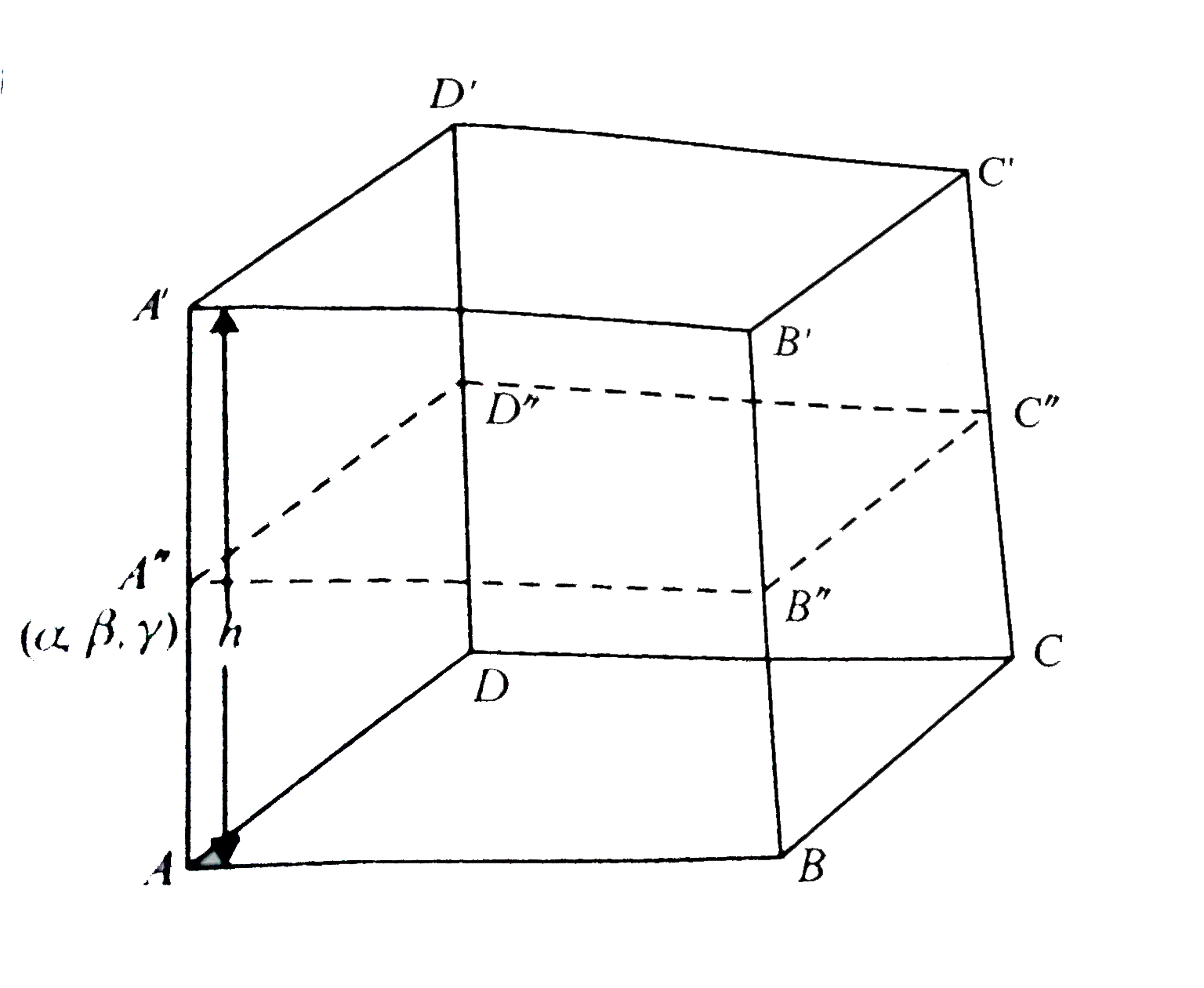Text Solution
Verified by Experts
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise ARCHIVES SINGLE CORRECT ANSWER TYPE|9 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise ARCHIVES MULTIPLE CORRECT ANSWERS TYPE|4 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise INTEGER TYPE|10 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise All Questions|291 VideosTRIGONOMETRIC EQUATIONS
CENGAGE PUBLICATION|Exercise Archives (Numerical value type)|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-THREE-DIMENSIONAL GEOMETRY -ARCHIVES SUBJECTIVE TYPE
- Find the equation of the plane passing through the points (2,1,0),(5...
Text Solution
|
- about to only mathematics
Text Solution
|
- A parallelepiped S has base points A ,B ,Ca n dD and upper face points...
Text Solution
|
- about to only mathematics
Text Solution
|
- A line with positive direction cosines passes through the point P(2, -...
Text Solution
|