Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LIMITS
CENGAGE PUBLICATION|Exercise EXERCISE 2.2|7 VideosLIMITS
CENGAGE PUBLICATION|Exercise EXERCISE 2.3|15 VideosLIMITS
CENGAGE PUBLICATION|Exercise Solved Examples|15 VideosJEE 2019
CENGAGE PUBLICATION|Exercise Chapter 10|8 VideosLINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
CENGAGE PUBLICATION|Exercise DPP 1.2|10 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-LIMITS-EXERCISE 2.1
- Evaluate lim(xto-2^(+)) (x^(2)-1)/(2x+4).
Text Solution
|
- Evaluate lim(xto2^(+)) ([x-2])/(log(x-2)), where [.] represents the gr...
Text Solution
|
- Evaluate lim(xto0) (sin[cosx])/(1+[cosx]) ([.] denotes the greatest in...
Text Solution
|
- If f(x)={{:((x-|x|)/(x)","xne0),(2", "x=0):},show that lim(xto0) f...
Text Solution
|
- Show that ("lim")(xrarr0) (e^(1/x)-1)/(e^(1/x)+1) does not exist
Text Solution
|
- Evaluate lim(x->0)(3x+|x|)/(7x-5|x|)
Text Solution
|
- If f(x)={{:(x","" "xlt0),(1","" "x=0),(x^(2)","" "xgt0):}," then find ...
Text Solution
|
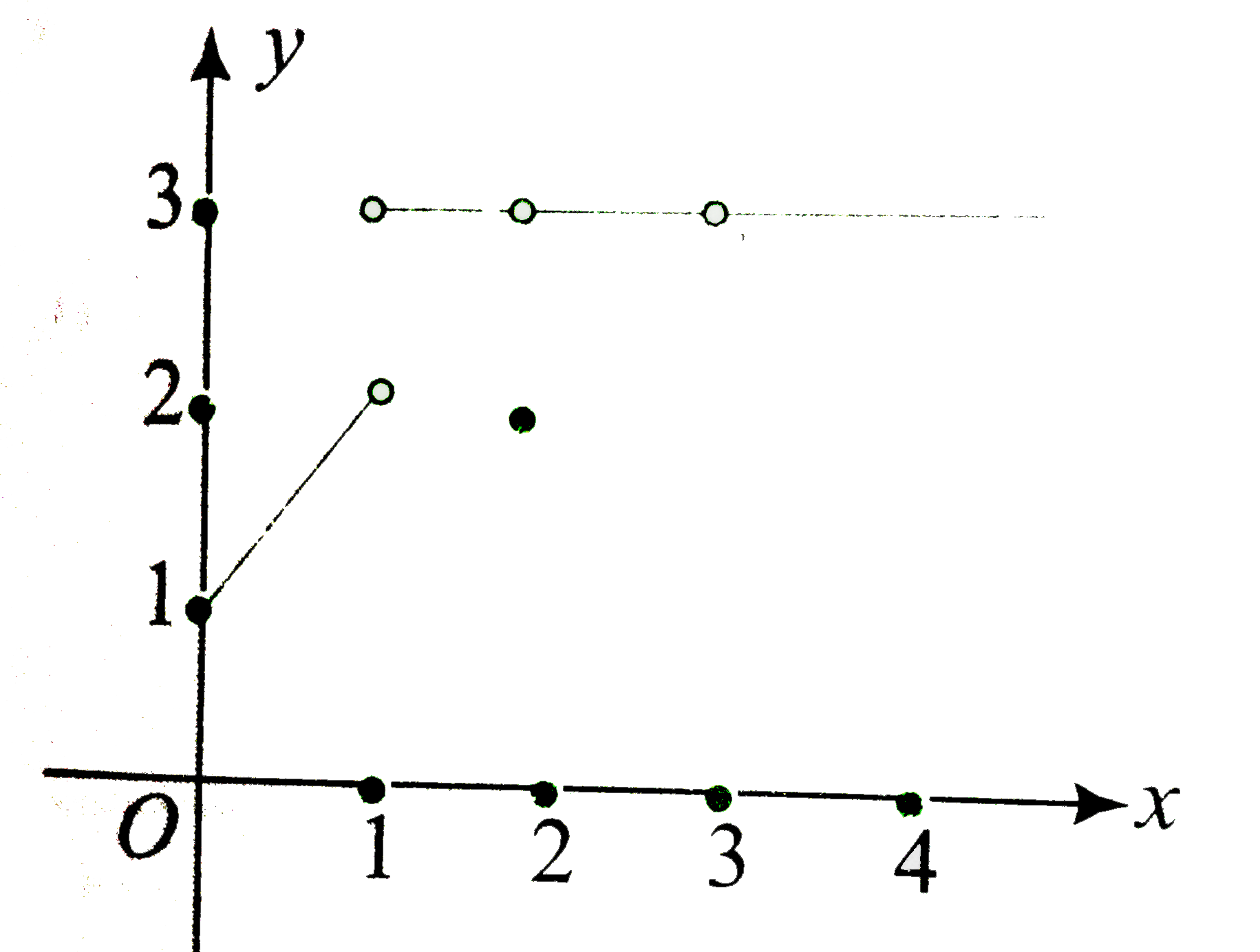
- Consider the following graph of the function y=f(x). Which of the foll...
Text Solution
|
- Evaluate lim(x to 0) (tan(sgn(x)))/(sgn(x)) if exists.
Text Solution
|
- If f(x)={sinx ,x!=npi,n in I2,ot h e r w i s e g(x)={x^2+1,x!=0,4,x=...
Text Solution
|