Text Solution
Verified by Experts
Topper's Solved these Questions
COORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Concept applications 1.1|6 VideosCOORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Concept applications 1.2|8 VideosCOORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Illustration1.67|1 VideosCOORDINATE SYSTEM
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 VideosCROSS PRODUCTS
CENGAGE PUBLICATION|Exercise DPP 2.2|13 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-COORDINATE SYSYEM -Solved examples
- If a ,b ,c are the p t h ,q t h ,r t h terms, respectively, of an HP ,...
Text Solution
|
- Prove that the circumcenter, orthocentre, incenter, and centroid of th...
Text Solution
|
- A rod of length k slides in a vertical plane, its ends touching the ...
Text Solution
|
- O X and O Y are two coordinate axes. On O Y a fixed point P(0,c) is t...
Text Solution
|
- If (x , y) and (X ,Y) are the coordinates of the same point referred t...
Text Solution
|
- What does the equation 2x^2+4x y-5y^2+20 x-22 y-14=0 become when re...
Text Solution
|
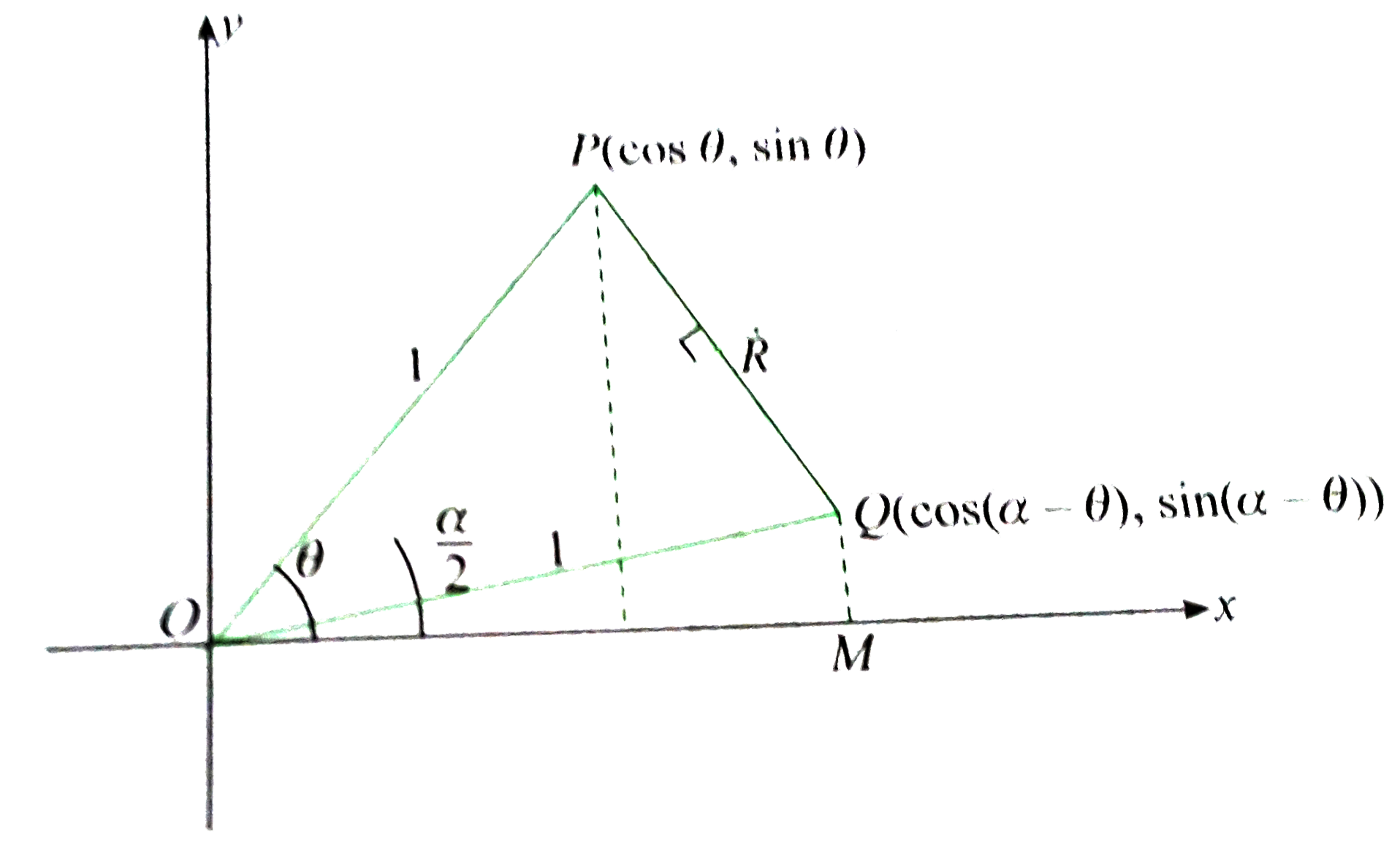
- Prove that the image of point P(costheta, sin theta) in the line havin...
Text Solution
|
- A line cuts the x-axis at A (7, 0) and the y-axis at B(0, - 5) A varia...
Text Solution
|
- Two straight lines rotate about two fixed points. If they start from t...
Text Solution
|