A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Multiple correct|13 VideosCOORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Linked|10 VideosCOORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Concept applications 1.6|9 VideosCOORDINATE SYSTEM
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 VideosCROSS PRODUCTS
CENGAGE PUBLICATION|Exercise DPP 2.2|13 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-COORDINATE SYSYEM -Exercises
- A particle p moves from the point A(0,4) to the point 10 ,-4) . The pa...
Text Solution
|
- If |x1y1 1x2y2 1x3y3 1|=|a1b1 1a2b2 1a3b3 1| then the two triangles ...
Text Solution
|
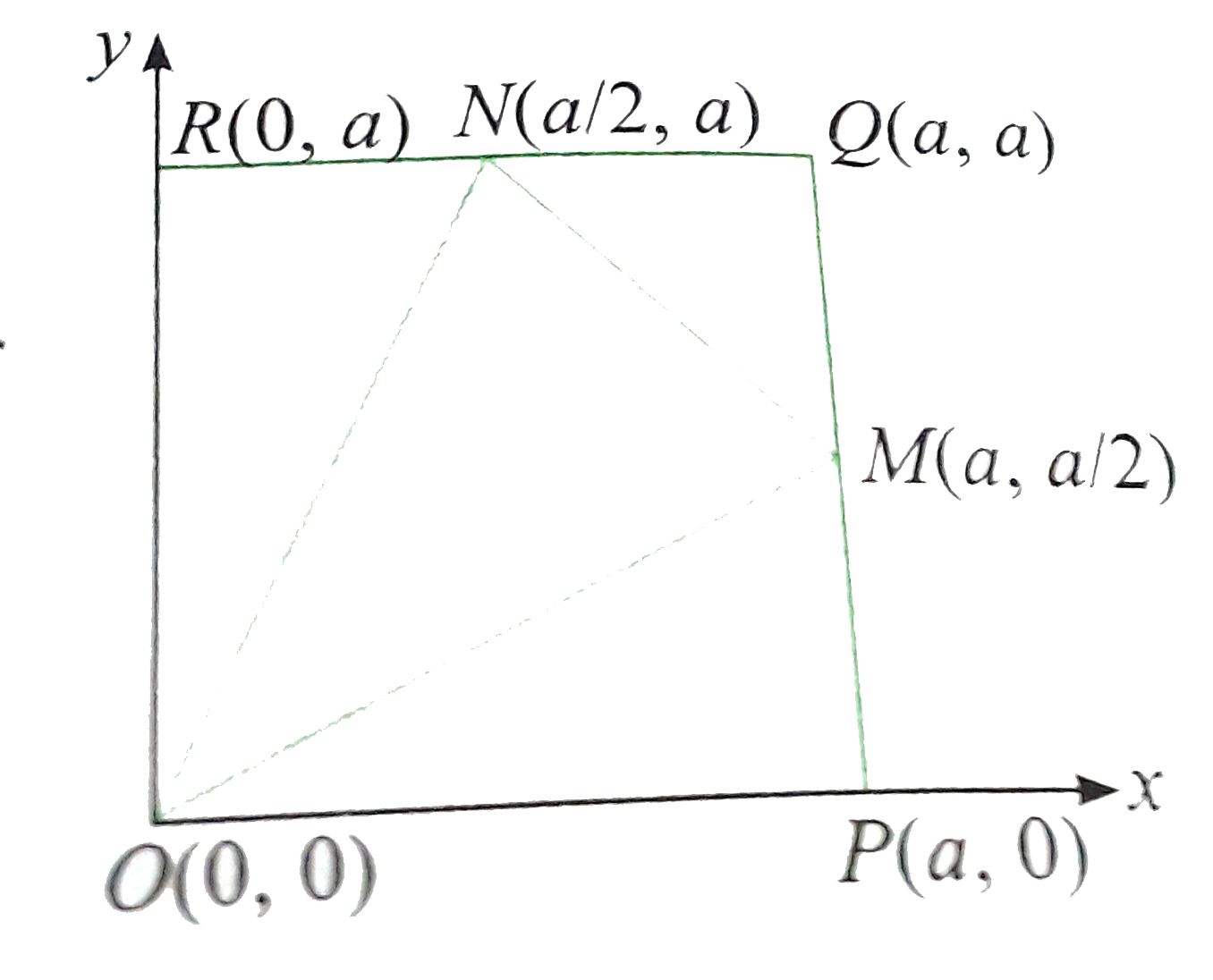
- O P Q R is a square and M ,N are the middle points of the sides P Qa n...
Text Solution
|
- A straight line passing through P(3,1) meets the coordinate axes at Aa...
Text Solution
|
- Let A-=(3,-4),B-=(1,2)dot Let P-=(2k-1,2k+1) be a variable point such ...
Text Solution
|
- The polar coordinates equivalent to (-3,sqrt3) are
Text Solution
|
- If the point P[X1+t(X2-X1),y1+t(y2-y1] divides AB internally where (X1...
Text Solution
|
- P and Q are points on the line joining A(-2,5) and B(3,1) such that A ...
Text Solution
|
- In triangle ABC, angle B is right angled, AC=2 and A(2,2), B(1,3) then...
Text Solution
|
- One vertex of an equilateral triangle is (2,2) and its centroid is (-2...
Text Solution
|
- ABCD is a rectangle with A(-1,2),B(3,7) and AB:BC=4:3. If P is the cen...
Text Solution
|
- If (2,-3), (6,5) and (-2,1) are three consecutive vertices of a rhombu...
Text Solution
|
- If poitns A(3,5) and B are equidistant from H(sqrt2,sqrt5) and B has r...
Text Solution
|
- Let n be the number of points having rational coordinates equidistant...
Text Solution
|
- In a triangle ABC the sides BC=5, CA=4 and AB=3. If A(0,0) and the int...
Text Solution
|
- If A(0, 0), B(1, 0) and C(1/2,sqrt(3)/2) then the centre of the circle...
Text Solution
|
- Statement 1: If in a triangle, orthocentre, circumcentre and centroid ...
Text Solution
|
- Consider three points P = (-sin (beta-alpha), -cos beta), Q = (cos(bet...
Text Solution
|
- If two vertices of a triangle are (-2,3) and (5,-1) the orthocentre li...
Text Solution
|
- The vertices of a triangle are (p q ,1/(p q)),(q r ,1/(q r)), and (r p...
Text Solution
|