Home
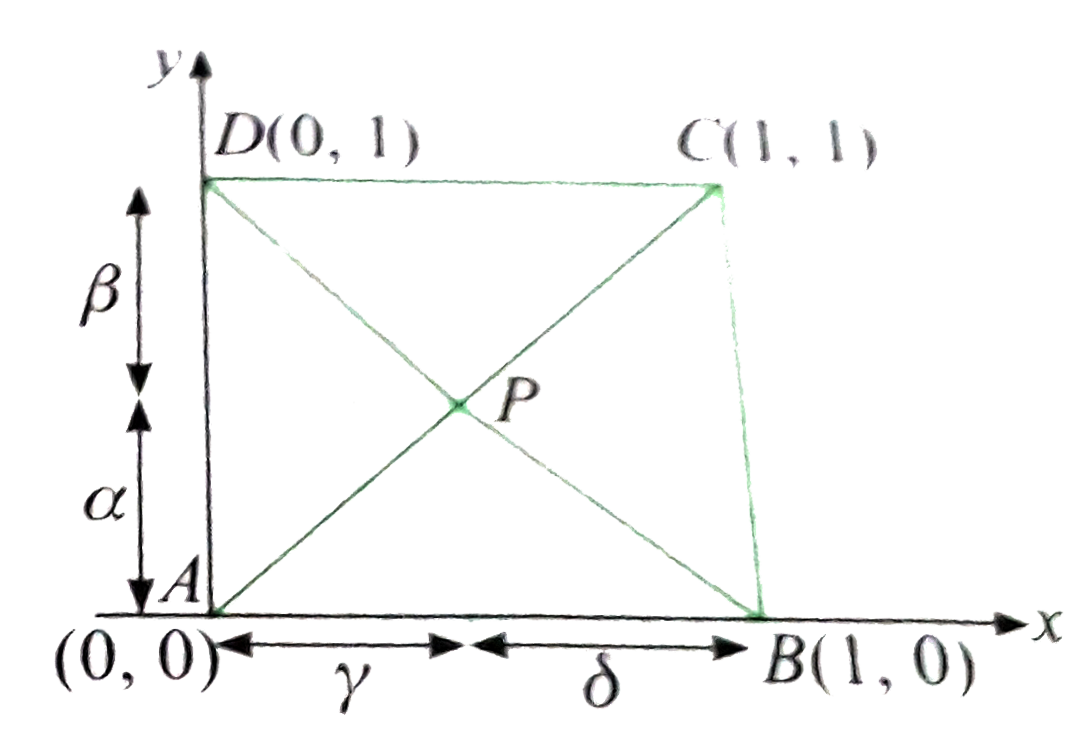
Class 12
MATHS
Let ABCD be a square with sides of unit ...

Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that `AE=AF`. Let P be a point inside the squre ABCD.
The value of `(PA)^2-(PB)^2+(PC)^2-(PD)^2` is equal to

A

3

B

2

C

1

D

0

Text Solution

Verified by Experts

The correct Answer is:
D

`(PA)^2-(PB)^2+(PC)^2-(PD)^2`
`=(alpha^2+gamma ^2)-(alpha^2+delta^2)+(delta^2+beta^2)-(gamma^2+beta^2)=0`
Promotional Banner

Topper's Solved these Questions

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Matrix match type|4 Videos

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Numerical value|12 Videos

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Multiple correct|13 Videos

  • COORDINATE SYSTEM

    CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 Videos

  • CROSS PRODUCTS

    CENGAGE PUBLICATION|Exercise DPP 2.2|13 Videos

Similar Questions

Explore conceptually related problems

Let ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD. The value of (PA)^(2)-(PB)^(2)+(PC)^(2)-(PD)^(2) is equal to -

Let ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD. The maximum area of quandrilateral CDFE will be -

Let ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE= AF. Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-

Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF . Let P be a point inside the squre ABCD. Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is

Let ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD. Let a line passing throught point A divides the square ABCD into two parts so that area of one part is double to another , then lenght of the line segment inside the square is -

P is an external point of the square ABCD. If PA gt PB ,then prove that PA^(2) - PB^(2) ~= PD^(2) - PC^(2)

ABCD is a square. E, F, G and H are the mid points of AB, BC, CD and DA respectively. Such that AE = BF = CG = DH . Prove that EFGH is a square.

In a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.

ABCD is a quadrilateral,AB and CD are parallel, P and Q are the midpoints of the sides BC and AD respectively. They, the value of bar(AB)+bar(DC) is -

In DeltaABC , D and E are two such points on the sides AB and AC respectively that DE||BC . If AD=x+3 , BD=3x+19 , AE=x and CE=3x+4 , then the value of x=