Text Solution
Verified by Experts
Topper's Solved these Questions
TRIGONOMETRIC FUNCTIONS
CENGAGE PUBLICATION|Exercise Concept Application Exercises 2.1|8 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE PUBLICATION|Exercise Concept Application Exercises 2.2|8 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE PUBLICATION|Exercise SINGLE CORRECT ANSWER TYPE|38 VideosTRIGONOMETRIC EQUATIONS
CENGAGE PUBLICATION|Exercise Archives (Numerical value type)|4 VideosTRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
CENGAGE PUBLICATION|Exercise Archives (Numerical Value Type)|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-TRIGONOMETRIC FUNCTIONS -example
- If 2cosx+sinx=1, then find the valie of 7x+6sinxdot
Text Solution
|
- If un=sin^("n")theta+cos^ntheta, then prove that (u4-u6)/(u2-u4)=1/2 .
Text Solution
|
- If a^2+b^2+2a bcostheta=1,c^2+a^2+2c dcostheta=1 and a c+b d+(a d+b c)...
Text Solution
|
- If (sec^4theta)/a+(tan^4theta)/b=1/(a+b), then prove that |b|lt=|a| .
Text Solution
|
- Let A=sinx+cosxdot Then find the value of sin^4x+cos^4x in terms of Ad...
Text Solution
|
- If x=(sin^3p)/(cos^2p),y=(cos^3p)/(sinp) and sinp+cosp=1/2 then find t...
Text Solution
|
- If (sinA)/(sinB)=(sqrt(3))/2 and (cosA)/(cosB)=(sqrt(5))/2, 0 < A, B <...
Text Solution
|
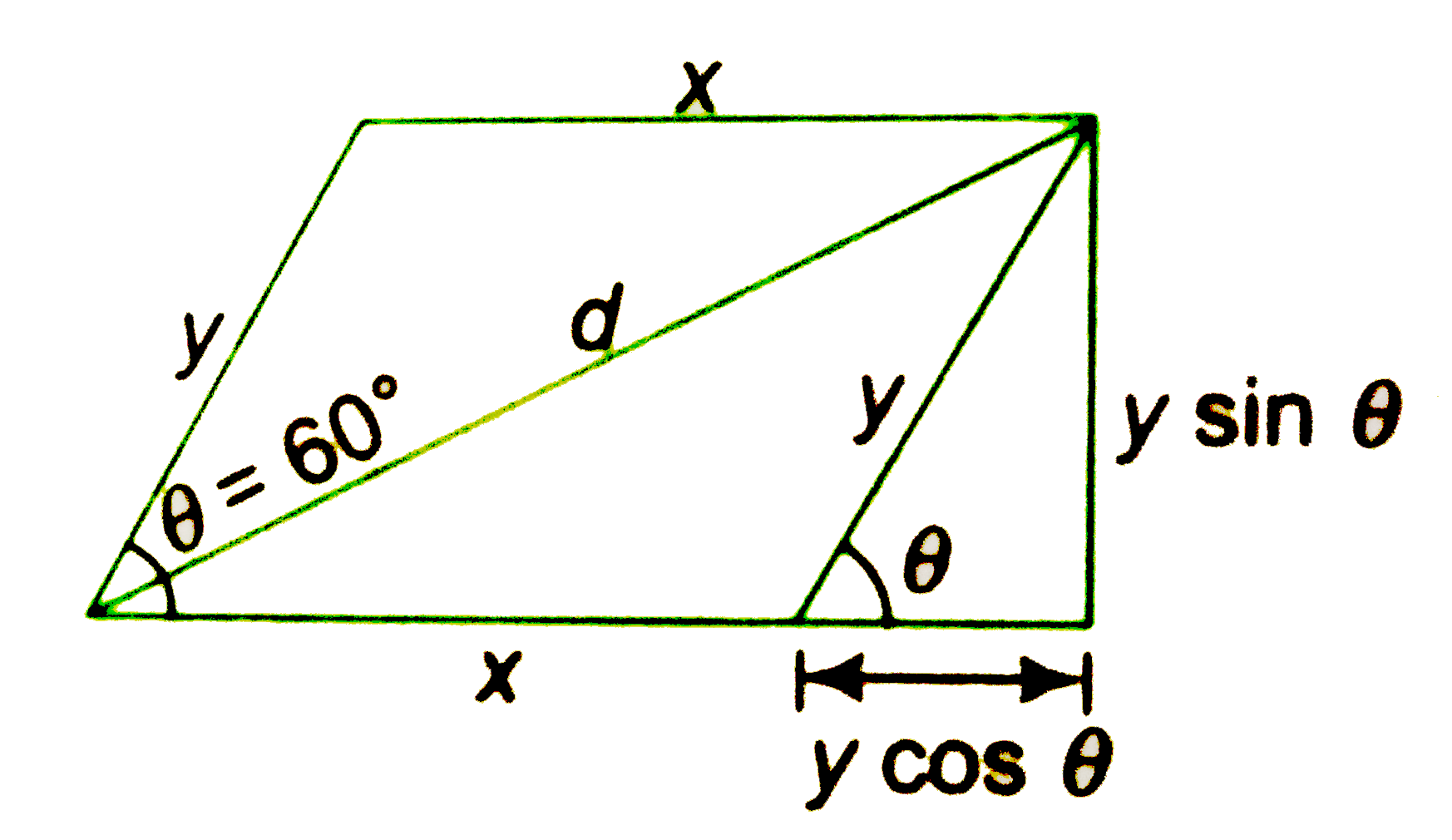
- A parallelogram containing a 60^0 angle has perimeter p and its longer...
Text Solution
|
- For each natural number ngt=2, prove that sinx1cosx2+sinx2cosx3+...+si...
Text Solution
|
- Find the range of y=sin^3x-6sin^2x+11sinx-6.
Text Solution
|