Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TRIGONOMETRIC FUNCTIONS
CENGAGE PUBLICATION|Exercise Concept Application Exercises 2.5|16 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE PUBLICATION|Exercise Concept Application Exercises 2.6|1 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE PUBLICATION|Exercise Concept Application Exercises 2.3|4 VideosTRIGONOMETRIC EQUATIONS
CENGAGE PUBLICATION|Exercise Archives (Numerical value type)|4 VideosTRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
CENGAGE PUBLICATION|Exercise Archives (Numerical Value Type)|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-TRIGONOMETRIC FUNCTIONS -Concept Application Exercises 2.4
- Let (-3, -4) be a point on the terminal side of theta. Find the sine, ...
Text Solution
|
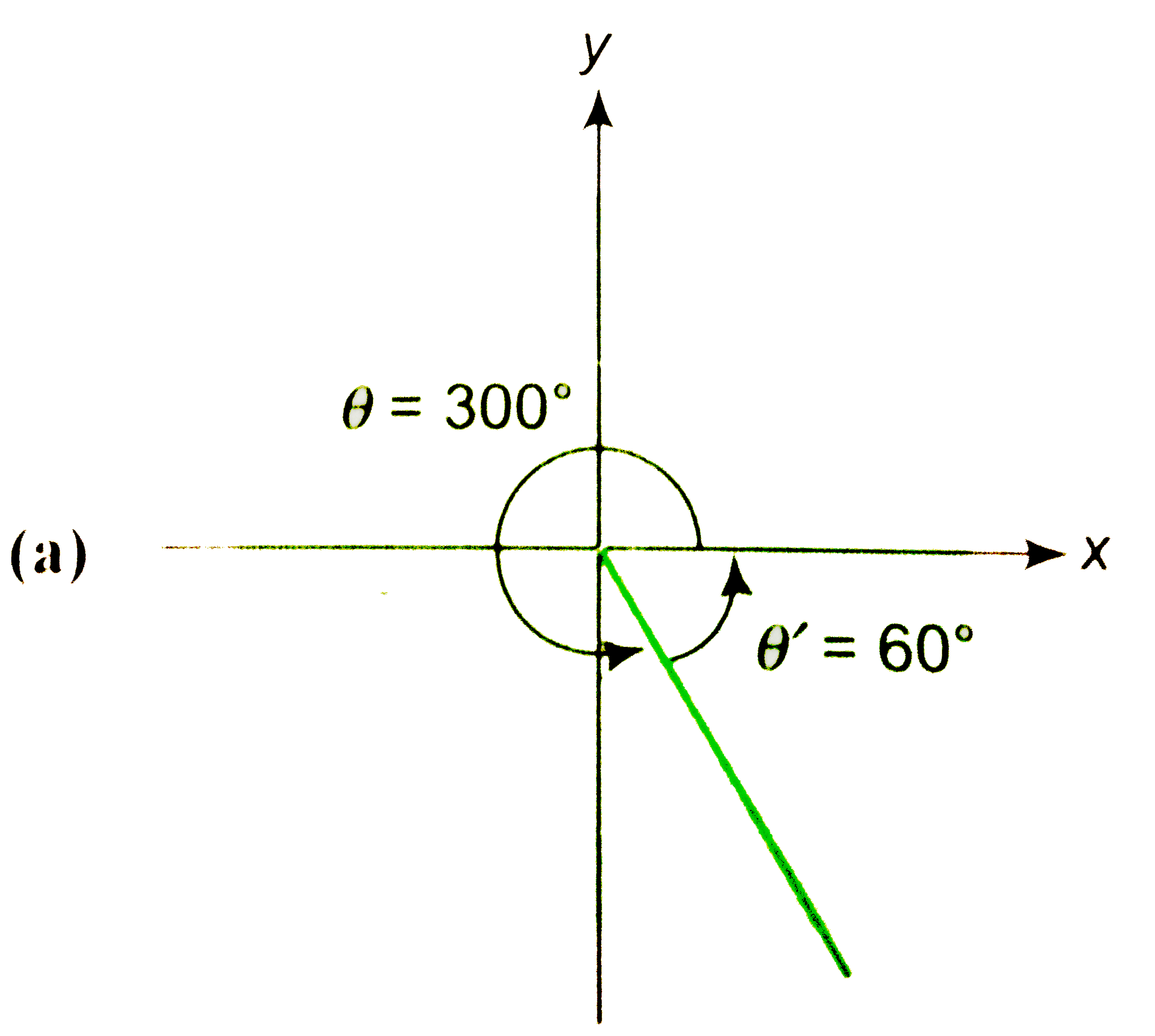
- Find the reference angle theta'for the following angles in standerd po...
Text Solution
|
- Evaluate each of the following trigonometric functions: " cosec.(...
Text Solution
|
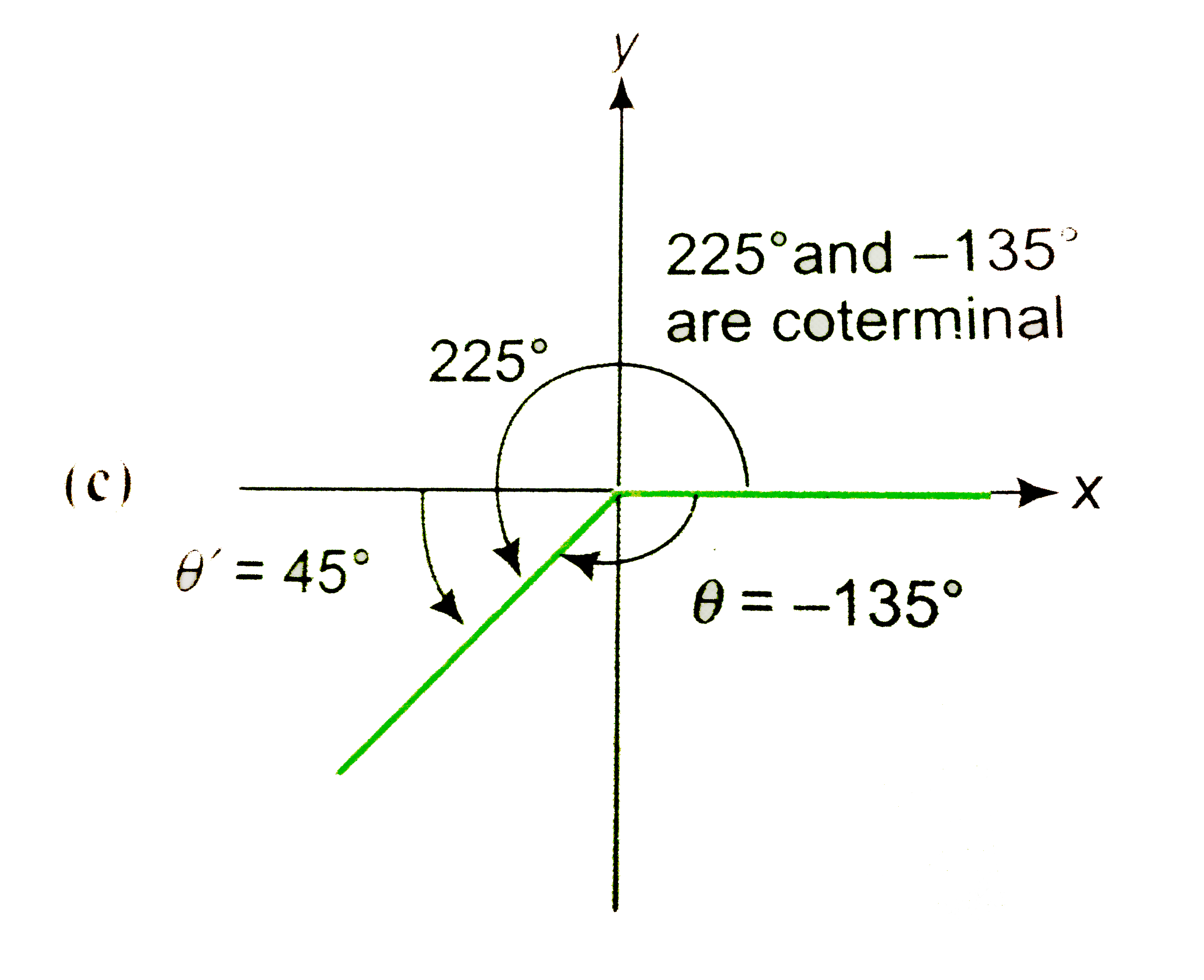
- State if the given pairs of angles are coterminal. (a) -185^@,535^...
Text Solution
|