A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PROGRESSION AND SERIES
CENGAGE PUBLICATION|Exercise Multiple Correct Answer|4 VideosPROGRESSION AND SERIES
CENGAGE PUBLICATION|Exercise ILLUSTRATION 5.1|1 VideosPROGRESSION AND SERIES
CENGAGE PUBLICATION|Exercise ARCHIVES (NUMERICAL VALUE TYPE )|8 VideosPROBABILITY II
CENGAGE PUBLICATION|Exercise MULTIPLE CORRECT ANSWER TYPE|6 VideosPROPERTIES AND SOLUTIONS OF TRIANGLE
CENGAGE PUBLICATION|Exercise Archives (Numerical Value Type)|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-PROGRESSION AND SERIES-Comprehension
- The 1^(st) , 2^(nd) and 3^(rd) terms of an arithmetic series are a, b ...
Text Solution
|
- The 1^(st) , 2^(nd) and 3^(rd) terms of an arithmetic series are a, b ...
Text Solution
|
- img src="https://d10lpgp6xz60nq.cloudfront.net/physicsimages/CENALGDPP...
Text Solution
|
- Let ABCD is a unit square and each side of the square is divided in th...
Text Solution
|
- <img src="https://d10lpgp6xz60nq.cloudfront.net/physicsimages/CENALGDP...
Text Solution
|
- Let f(n) denote the n^(th) terms of the seqence of 3,6,11,18,27,…. and...
Text Solution
|
- Let f(n) denote the n^(th) terms of the seqence of 3,6,11,18,27,…. and...
Text Solution
|
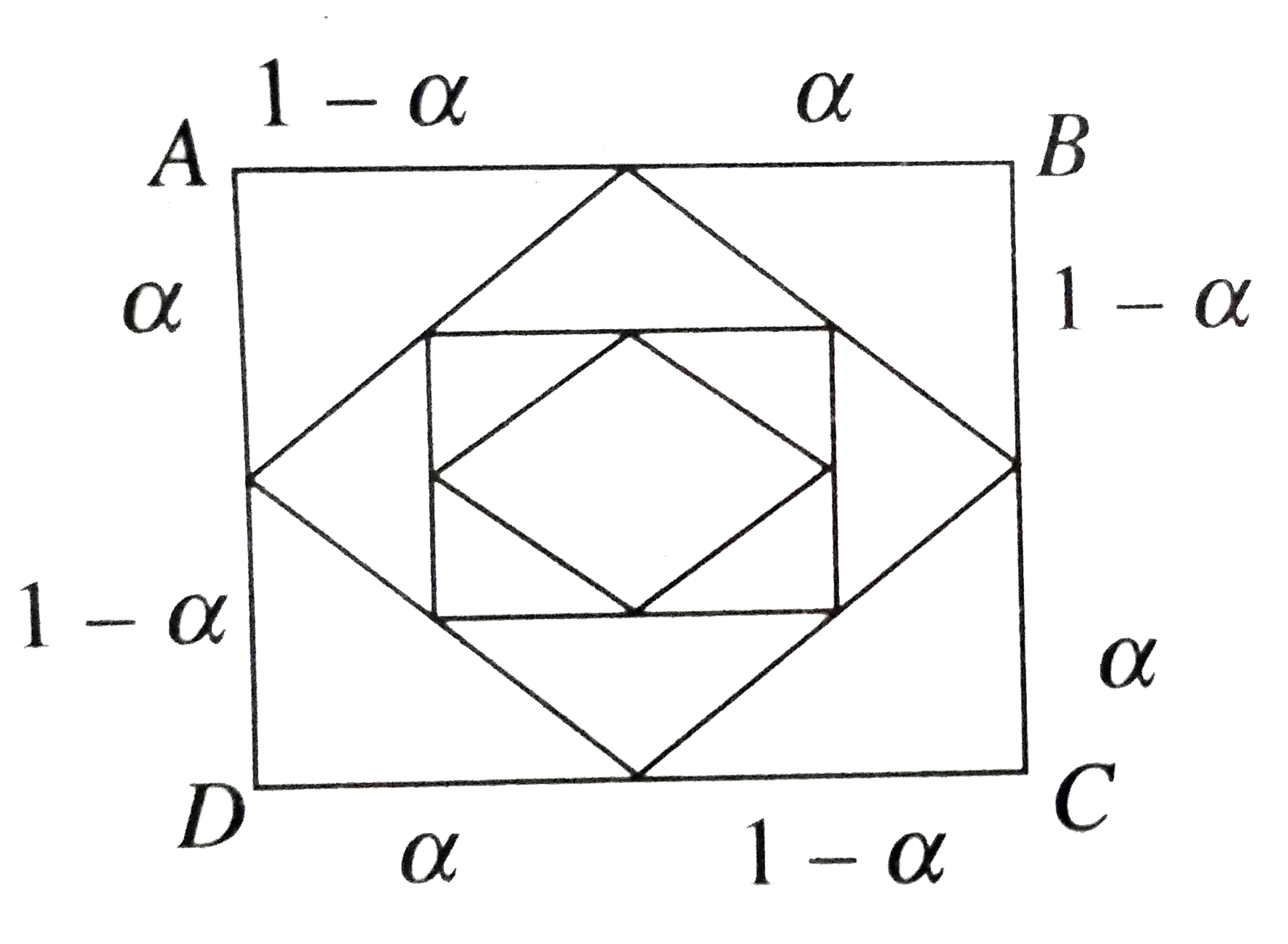
 Let `ABCD` is a unit square and each side of the square is divided in the ratio `alpha : (1-alpha) (0 lt alpha lt 1)` . These points are connected to obtain another square. The sides of new square are divided in the ratio `alpha : (1-alpha)` and points are joined to obtain another square. The process is continued idefinitely. Let `a_(n)` denote the length of side and `A_(n)` the area of the `n^(th)` square
Let `ABCD` is a unit square and each side of the square is divided in the ratio `alpha : (1-alpha) (0 lt alpha lt 1)` . These points are connected to obtain another square. The sides of new square are divided in the ratio `alpha : (1-alpha)` and points are joined to obtain another square. The process is continued idefinitely. Let `a_(n)` denote the length of side and `A_(n)` the area of the `n^(th)` square