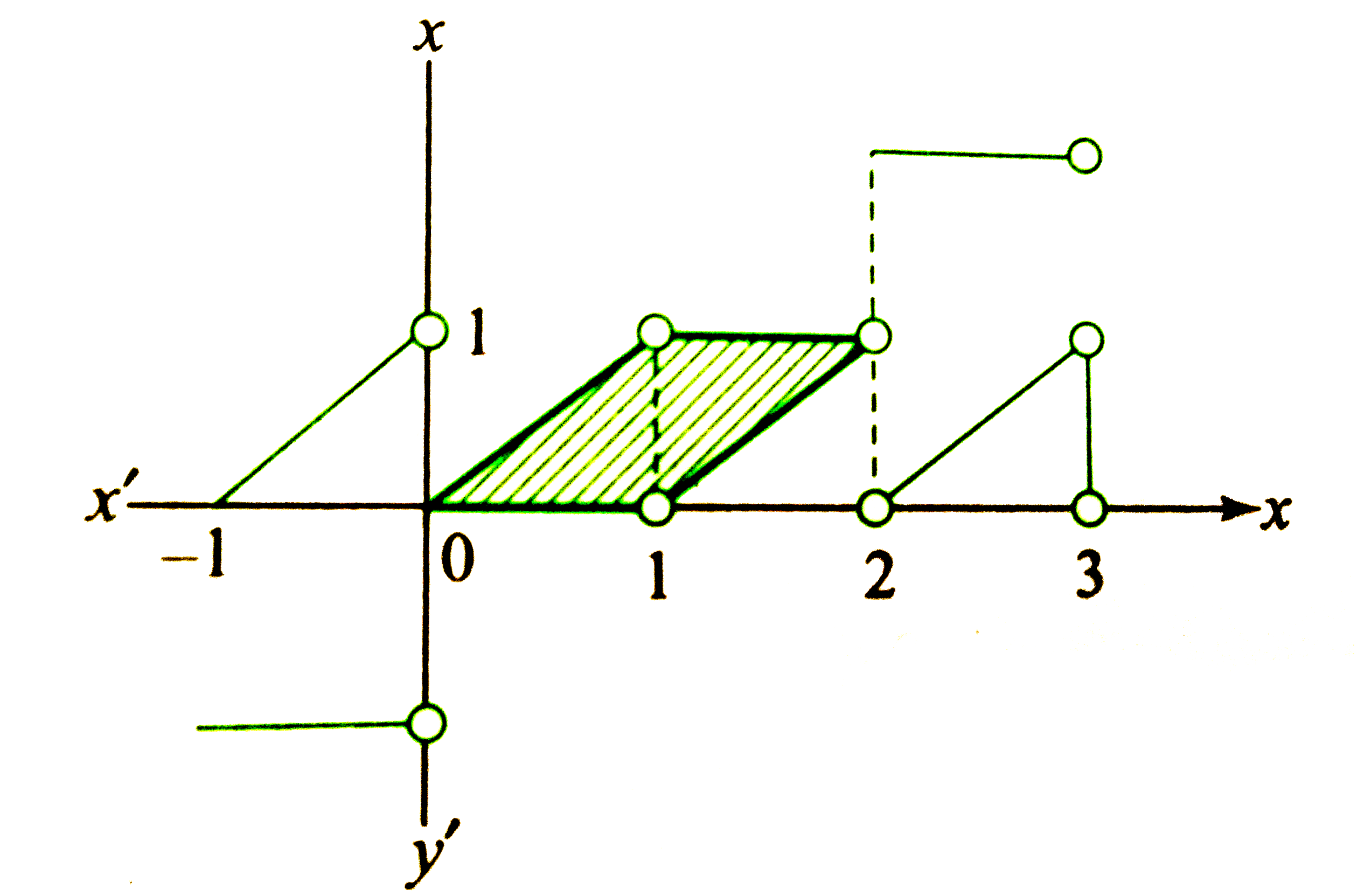
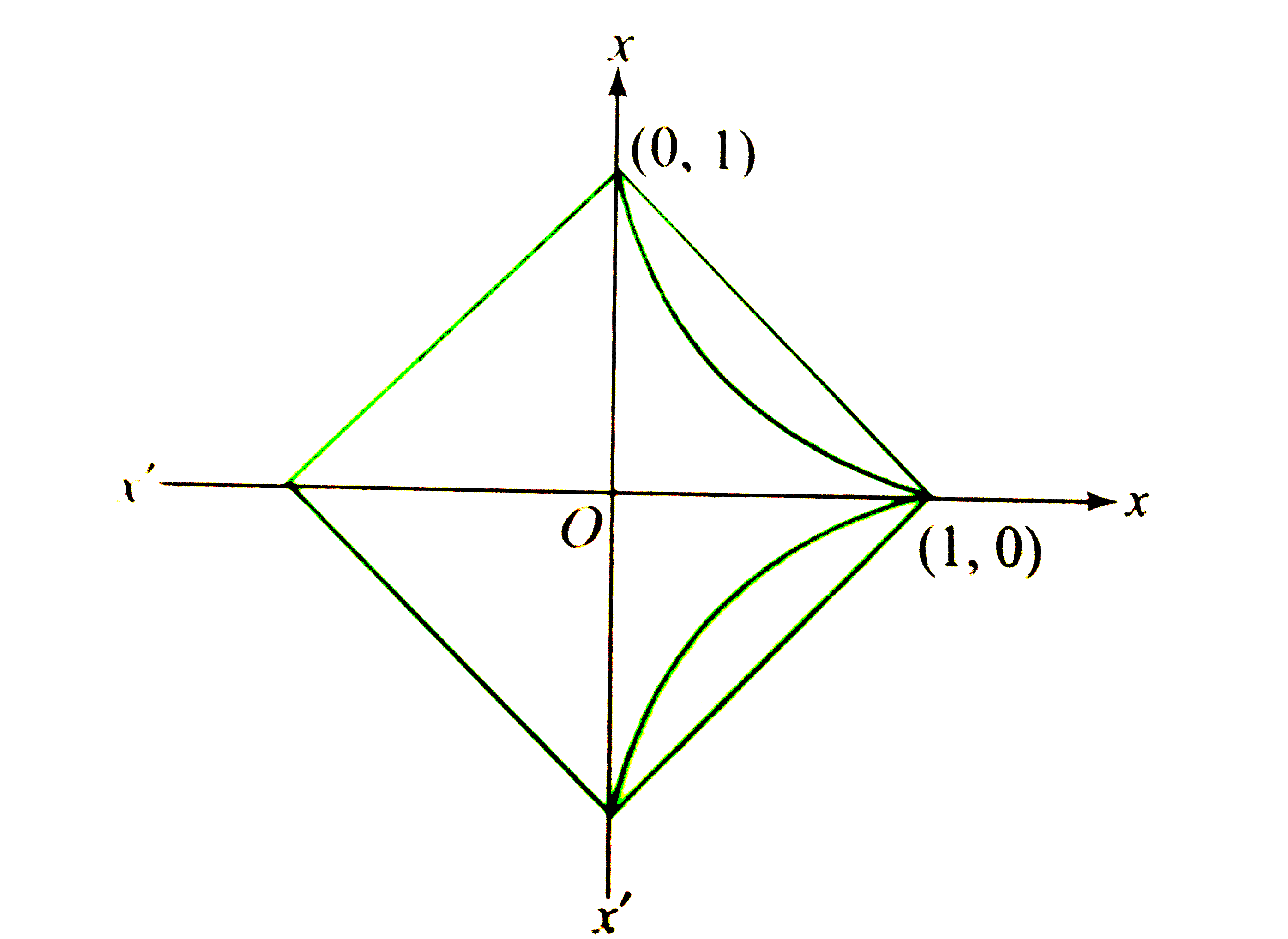
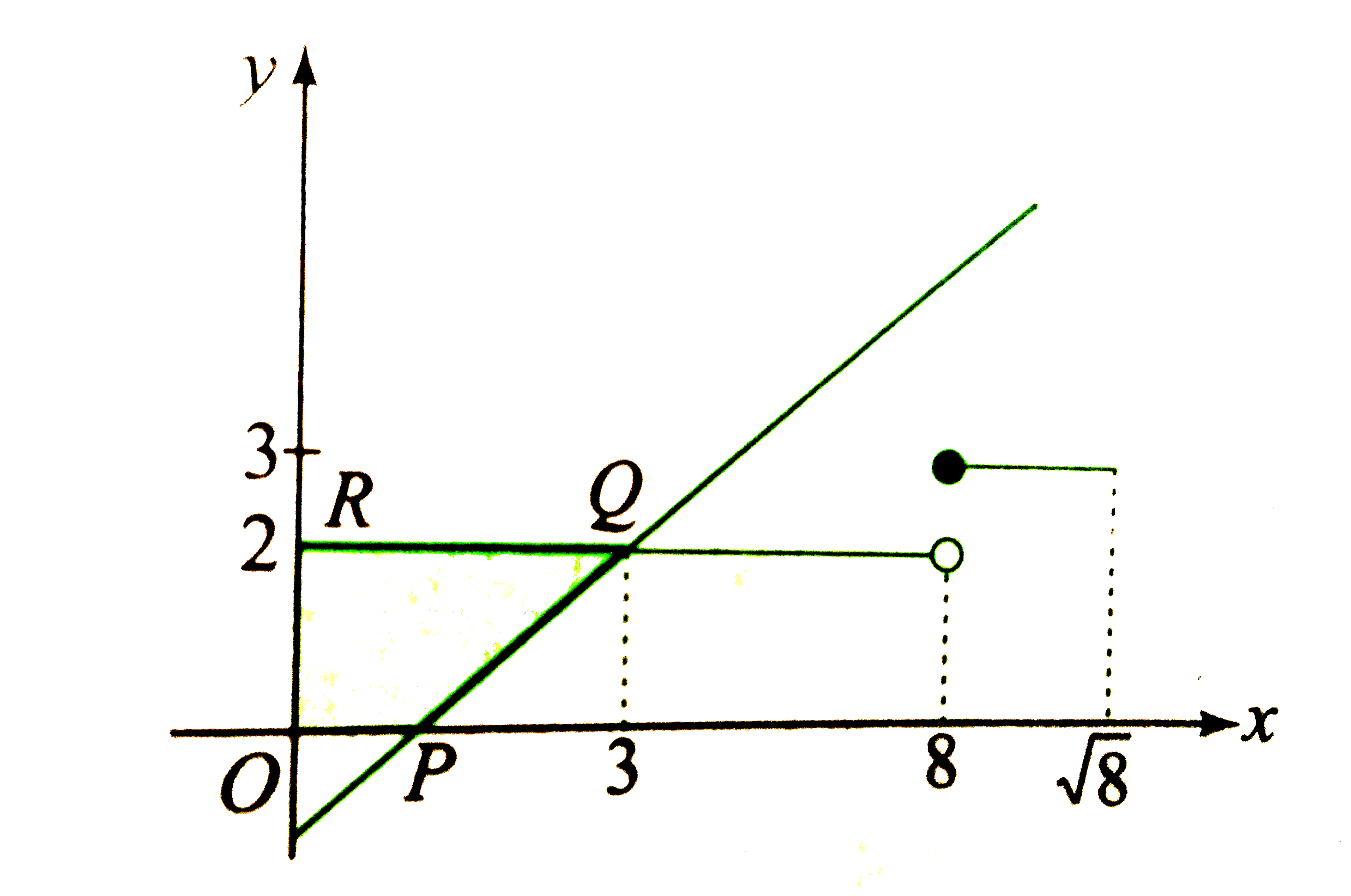
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
AREA
CENGAGE PUBLICATION|Exercise Numerical Value Type|18 VideosAREA
CENGAGE PUBLICATION|Exercise Archives|10 VideosAREA
CENGAGE PUBLICATION|Exercise Linkded Comprehension Type|21 VideosAPPLICATIONS OF DERIVATIVES
CENGAGE PUBLICATION|Exercise Subjective Type|2 VideosBINOMIAL THEOREM
CENGAGE PUBLICATION|Exercise Comprehension|11 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-AREA-Matrix Match Type
- Match the following lists :
Text Solution
|
- show that the tangents to the curve y=2x^3-3 at the point where x=2 a...
Text Solution
|
- find the point on the curve y=2x^2-6x-4 at which the tangent is parall...
Text Solution
|
- Find the point on the curve y=x^3-11 x+5 at which the tangent ha...
Text Solution
|
- find the equation of the tangent to the curve y=-5x^2+6x+7 at the poin...
Text Solution
|