Home
Class 12
MATHS
The straight line (x)/(4)+(y)/(3) =1 int...

The straight line `(x)/(4)+(y)/(3) =1` intersects the ellipse `(x^(2))/(16)+(y^(2))/(9) =1` at two points A and B, there is a point P on this ellipse such that the area of `DeltaPAB` is equal to `6(sqrt(2)-1)`. Then the number of such points (P) is/are

A

0

B

1

C

2

D

3

Text Solution

Verified by Experts

The correct Answer is:
D
Let the perpendicular distance of P from the line be h,

`:. (1)/(2) xx h xx 5 = 6 (sqrt(2)-1)`
`:. h = (12)/(5) (sqrt(2)-1)`
Also tangent parallel to the given line is `4y + 3x = 12 sqrt(2)`
Its distance from the line `4y +3x = 12` is `h =(12)/(5) (sqrt(2)-1)` Hence there are three points as shown in the figure.
Promotional Banner

Topper's Solved these Questions

  • ELLIPSE

    CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|6 Videos

  • DOT PRODUCT

    CENGAGE PUBLICATION|Exercise DPP 2.1|15 Videos

  • EQAUTION OF STRAIGHT LINE AND ITS APPLICATION

    CENGAGE PUBLICATION|Exercise DPP 3.2|13 Videos

Similar Questions

Explore conceptually related problems

The line y=2t^(2) intersects the ellipse (x^(2))/(9)+(y^(2))/(4)=1 in real points if

The line x =2 y intersects the ellipse (x^(2))/(4) +y^(2) = 1 at the points P and Q . The equation of the circle with pq as diameter is _

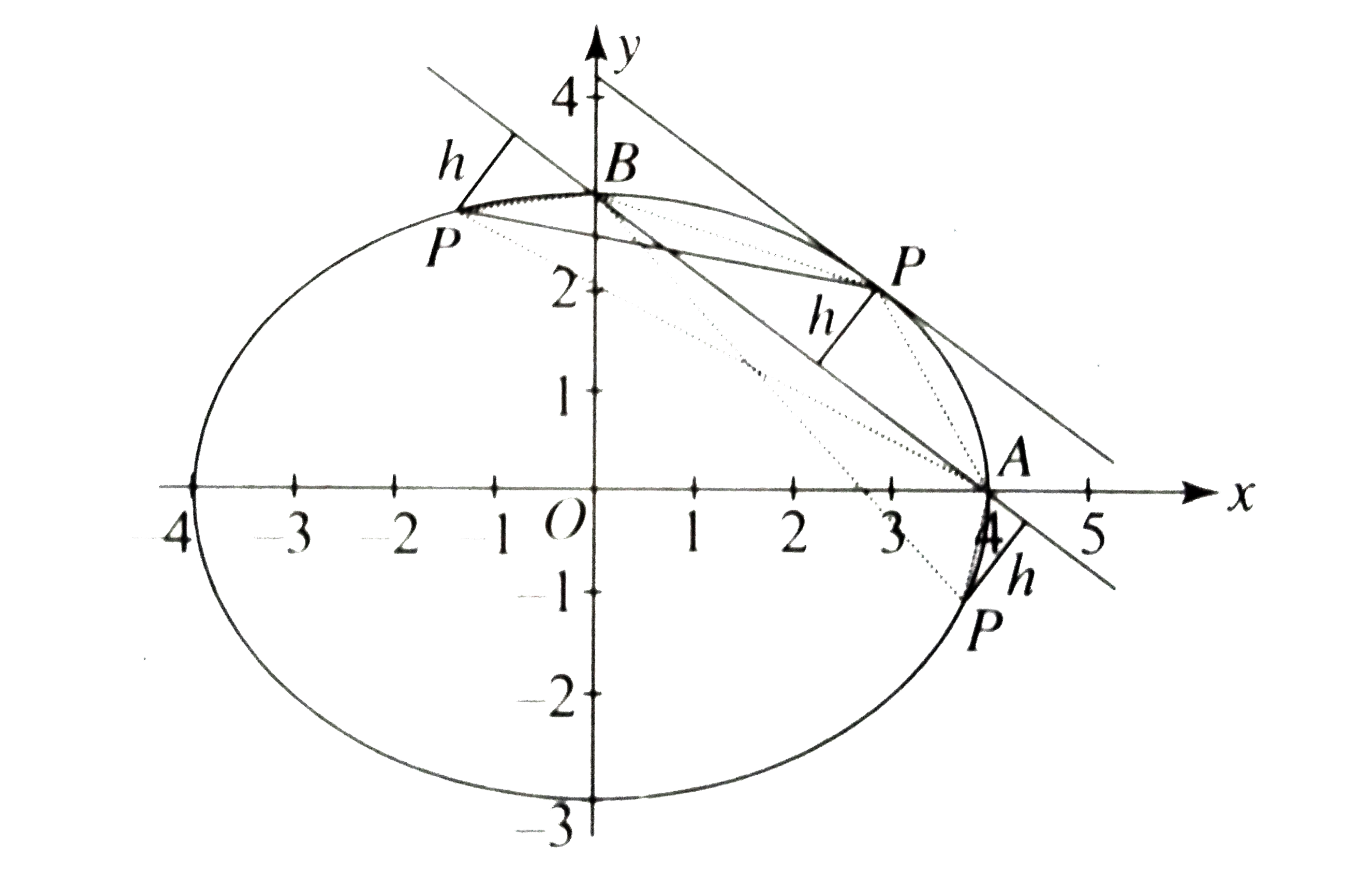
The straight line x + y = a will be a tangent to the ellipse (x^(2))/(9) + (y^(2))/(16) = 1 if the value of a is -

Prove that SP + S'P = 20 for the ellipse (x^(2))/(100) + (y^(2))/(36) = 1 , S and S' are the two foci of the ellipse and P is any point on the ellipse

Lines x + y = 1 and 3y = x + 3 intersect the ellipse x^(2) + 9y^(2) = 9 at the points P , Q , R . The area of the triangle PQR is _

The line y = x intersects the hyperbola (x^(2))/(9) -(y^(2))/(25) = 1 at the points P and Q . The eccentricity of ellipse with PQ as major axis and minor axis of length (5)/(sqrt(2)) is _

Let the foci of the ellipse (x^(2))/(9) + y^(2) = 1 subtend a right angle at a point P . Then the locus of P is _

Dentermine the position of the point (2,-3) with respect to the ellipse (x^(2))/(9) +(y^(2))/(25) = 1 .

Let P be a point on the ellipse (x^(2))/(16) + (y^(2))/(9) = 1 . If the distance of P from centre of the ellipse be equal with the average value of semi major axis and semi minor axis, then the coordinates of P is _

Find the points on the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 such that the tangent at each point makes equal angles with the axes.