Home
Class 12
MATHS
Find the middle point of the chord of th...

Find the middle point of the chord of the circle `x^2+y^2=25` intercepted on the line `x-2y=2`

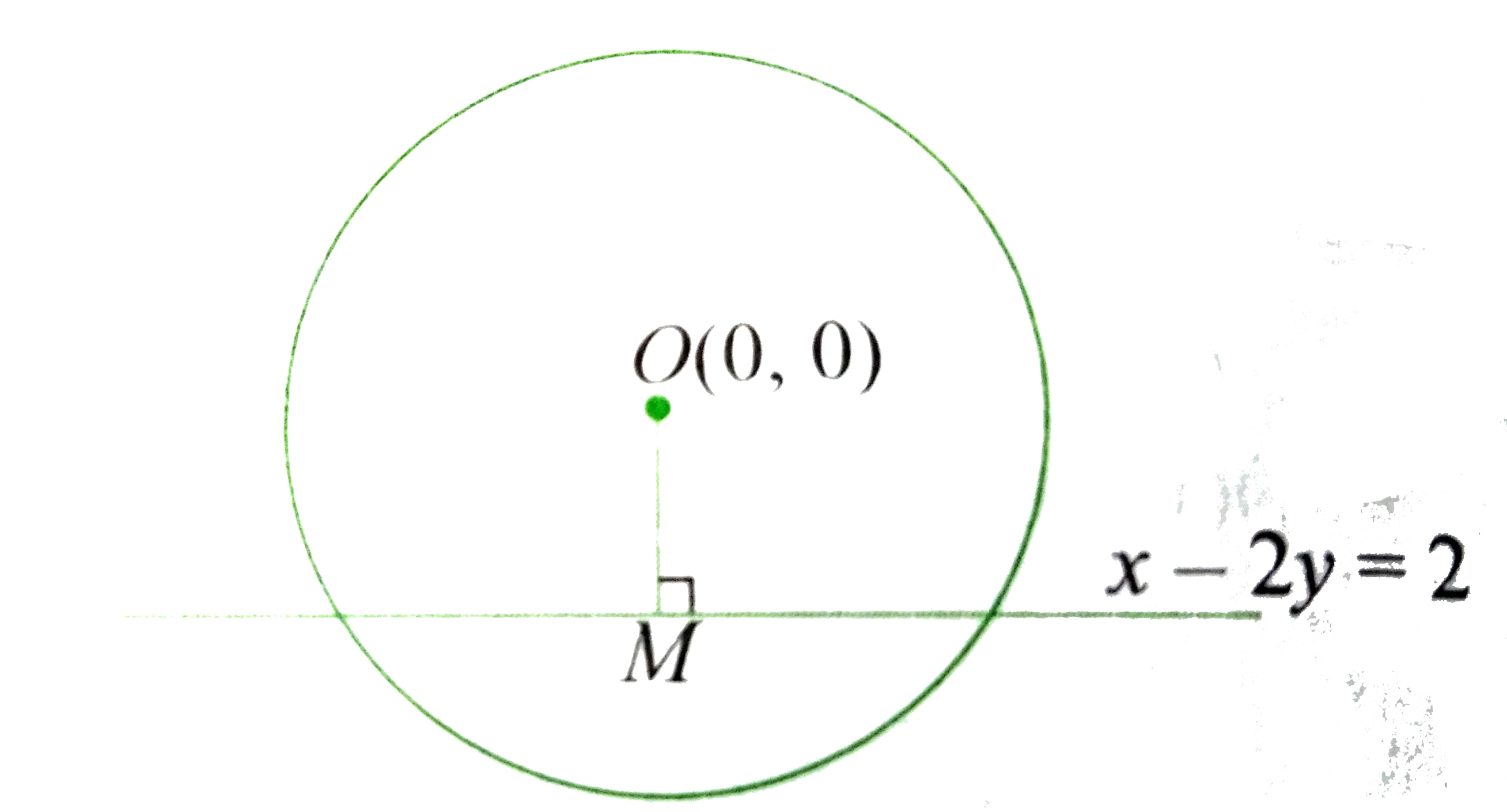
Text Solution

Verified by Experts

The correct Answer is:
`(2//5,-4//5)`

Let the middle point of chord be M(h,k) .
So, equation of OM is `2x+y=0`.
Solving this line with chord `x-2y=2`, we get point M as `(2//5,-4//5)`.
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.19|1 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.20|1 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.14|4 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Find the length of the chord intercepted by the circle x^2+y^2-6x+8y-5=0 on the line 2x-y=5.

Find the locus of the mid point of the chord of the circle x^2+y^2=a^2 which subtend a right angle at the point (0,0).

The equation of the locus of the middle point of a chord of the circle x^2+y^2=2(x+y) such that the pair of lines joining the origin to the point of intersection of the chord and the circle are equally inclined to the x-axis is (a) x+y=2 (b) x-y=2 (c) 2x-y=1 (d) none of these

Find the coordinates of the middle point of the portion of the straight line 2x+y=4 intercepted between the x and the y - axes.

Find the equation of the chord of the circle x^2+y^2=9 whose middle point is (1,-2)

Find the equation of the chord of the circle x^2+y^2=a^2 passing through the point (2, 3) farthest from the center.

Find the locus of the-mid points of the chords of the circle x^2 + y^2=16 , which are tangent to the hyperbola 9x^2-16y^2= 144

Find the equation of the normal to the circle x^2+y^2-2x=0 parallel to the line x+2y=3.

Find the locus of the midpoint of the chords of the circle x^2+y^2-ax-by=0 which subtend a right angle at the point (a/2 ,b/2)dot is

Find the locus of the mid points of the chords of the circle x^2 + y^2 -2x -6y - 10 = 0 which pass through the origin.