Home
Class 12
MATHS
Let A be the centre of the circle x^2+y^...

Let A be the centre of the circle `x^2+y^2-2x-4y-20=0` Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD

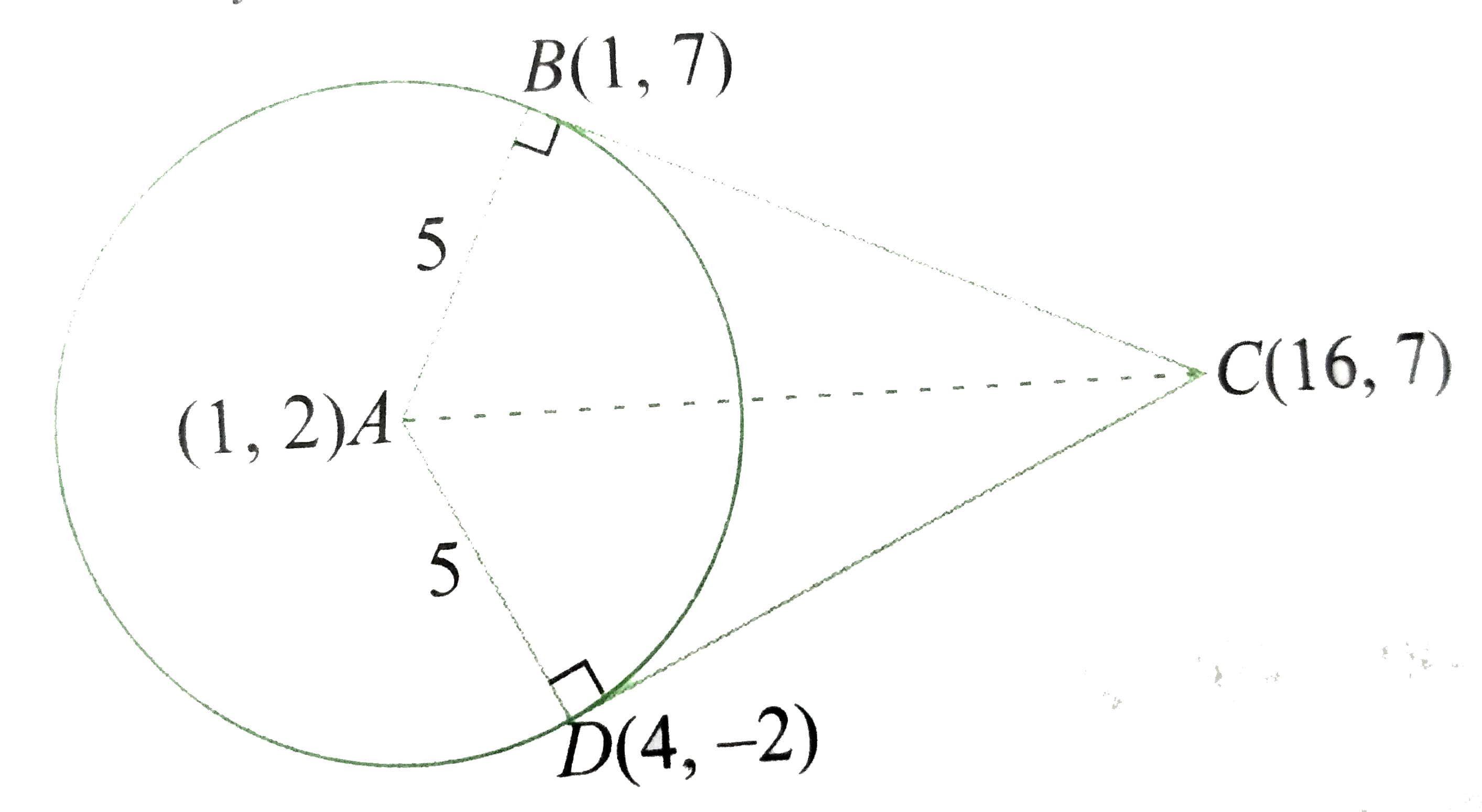
Text Solution

Verified by Experts

The correct Answer is:
75 sq. units
The equation of the circle is
`x^(2)+y^(2)-2x-4y-20=0`
Center `-= (1,2) ` radius `=sqrt(1+4+20)=5`
The equation of tangent at `(1,7)` is
`x.1+y.7-(x+1)-2(y+7)-20=0`
or `y-7=0 ` (1)
Similarly, the equation of tangent at (4,-1) is
`4x-2y-(x+4)-2(y-2)-20=0`
or `3x-4y-20=0` (2)

For point C, solving (1) and (2), we get `x=16` and `y=7` . Therefore, `C-= (16,7)`
Now, clearly ,
ar(quad. BCDA) `=2 xx ` ar (`Delta ABC)`
`=2 xx (1)/(2) xx AB xx BC`
`=AB xx BC`
where `AB=` Radius of circle `=5`
and `BC=15`
`:. ` ar (quad. ABCD) `= 5 xx 15=75 sq.` units
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.12|4 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.13|4 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.10|5 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Let A be the centre of the circle x^(2)+y^(2)-2x-4y-20=0 . Let B(1,7) and (4,-2) be two points on the circle such that tangents at B and D meet at C. The area of the quadrilateral ABCD is

Find the points on the circle x^2+y^2-2x+4y-20=0 which are the farthest and nearest to the point (-5,6)dot

From a point P on the normal y=x+c of the circle x^2+y^2-2x-4y+5-lambda^2-0, two tangents are drawn to the same circle touching it at point Ba n dC . If the area of quadrilateral O B P C (where O is the center of the circle) is 36 sq. units, find the possible values of lambdadot It is given that point P is at distance |lambda|(sqrt(2)-1) from the circle.

The length of the tangent of the circle x^2+y^2-2x-y -7 = 0 from the point (-1,-3) is

Find the point of intersection of the circle x^2+y^2-3x-4y+2=0 with the x-axis.

The common tangents to the circle x^(2)+y^(2)=2 and the parabola y^(2)=8x touch the circle at the points P, Q and the parabola at the points R, S. Then the area of the quadrilateral PQSR is

The line 2x-y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x-2y=4 . Then find the radius of the circle.

Find the centre and the radius of the circle. 2x^2+2y^2-4x+8y-4=0

The lngth of the tangent from the point (1, 1) to the circle x^2 + y^2 + 4x + 6y + 1 = 0 is

If tangent at (1, 2) to the circle C_1: x^2+y^2= 5 intersects the circle C_2: x^2 + y^2 = 9 at A and B and tangents at A and B to the second circle meet at point C, then the co- ordinates of C are given by