Home
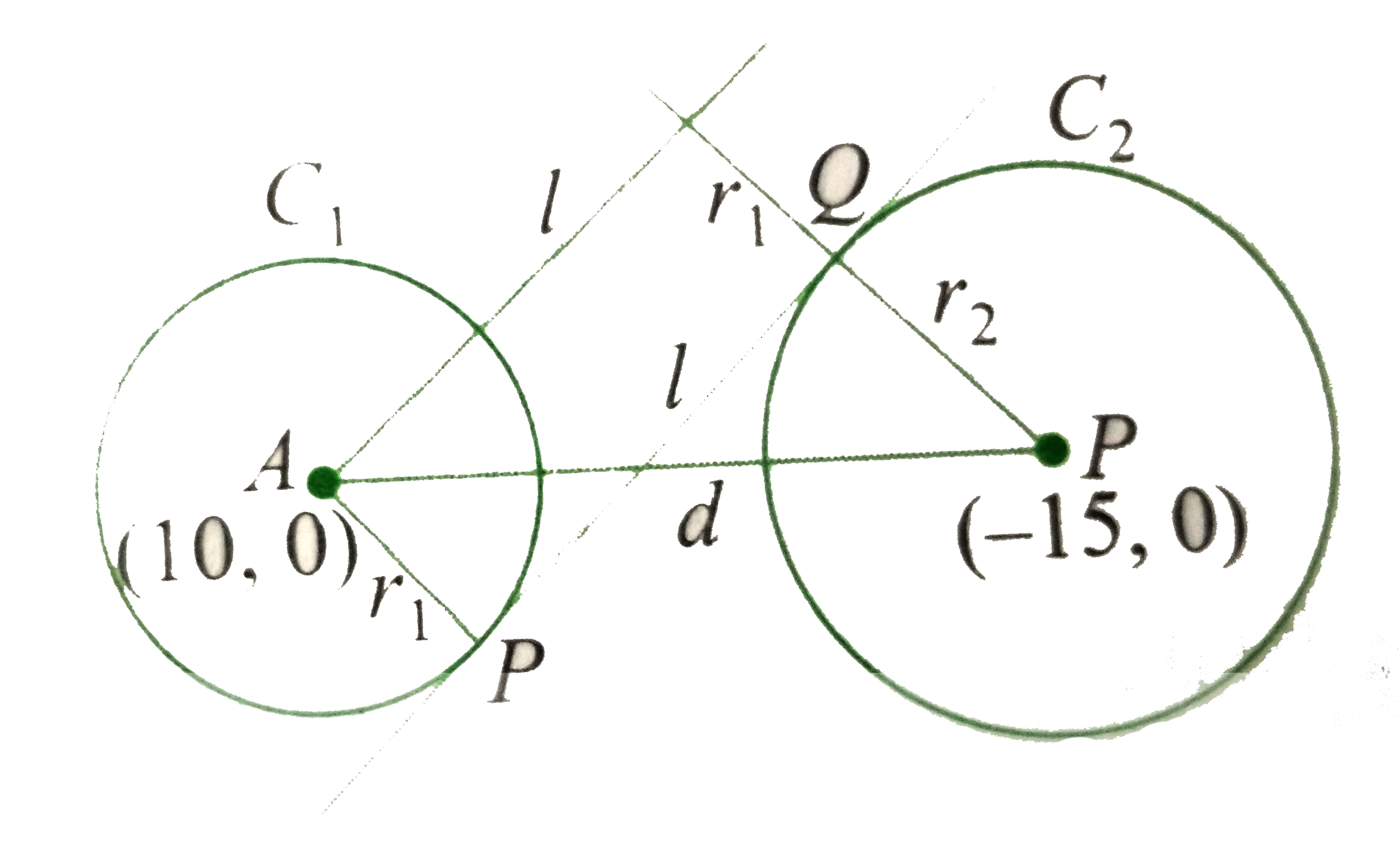
Class 12
MATHS
Let C1 and C2 are circles defined by x...

Let `C_1 and C_2` are circles defined by `x^2+y^2 -20x+64=0` and `x^2+y^2+30x +144=0`. The length of the shortest line segment PQ that is tangent to `C_1` at P and to `C_2` at Q is

A

20

B

15

C

22

D

27

Text Solution

Verified by Experts

The correct Answer is:
1
The centers are `(10,0)` and `(-15,0)`
and the radii are `r_(1)=6` and `r_(2)=9`
Also, `d=25,r_(1)+r_(2) lt d`.

So, the circle are neither intersecting nor touching. Therefore,
`PQ= sqrt(d^(2)-(r_(1)+r_(2))^(2))`
`=sqrt(625-225)`
`=20`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Multiple Correct Anser Type|29 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Linked Comprehension Type (For Problem 1-3)|3 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.17|2 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Let C_1 and C_2 be two circles whose equations are x^2+y^2-2x=0 and x^2+y^2+2x=0 and P(lambda, lambda) is a variable point . List 1 a) P lies inside C_1 ​ but outside C_2 ​ b)P lies inside C_2 ​ but outside C_1 ​ c)P lies outside C_1 ​ but outside C_2 ​ d)P does not lie inside C_2 ​ List 2 p)λ ϵ (−∞,−1)∪(0,∞) q)λ ϵ (−∞,−1)∪(1,∞) r)λ ϵ (−1,0) s)λ ϵ (0,1)

Let C_(1) and C_(2) denote the centres of the circles x^(2) +y^(2) = 4 and (x -2)^(2) + y^(2) = 1 respectively and let P and Q be their points of intersection. Then the areas of triangles C_(1) PQ and C_(2) PQ are in the ratio _

If the straight line x - 2y + 1 = 0 intersects the circle x^2 + y^2 = 25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x^2 + y^2 = 25 .

If C_1,C_2,a n dC_3 belong to a family of circles through the points (x_1,y_1)a n d(x_2, y_2) prove that the ratio of the length of the tangents from any point on C_1 to the circles C_2a n dC_3 is constant.

Find the condition if the circle whose equations are x^2+y^2+c^2=2a x and x^2+y^2+c^2-2b y=0 touch one another externally.

If the circles x^2+y^2+2ax+c^2=0 and x^2+y^2+2by+c^2=0 touch each other,prove that 1/a^2+1/b^2=1/c^2

If the circles x^2+y^2+2a x+c y+a=0 and x^2+y^2-3a x+d y-1=0 intersects at points P and Q , then find the values of a for which the line 5x+b y-a=0 passes through Pa n dQdot

Let x^2 +y^2 -2x-2y-2=0 and x^2 +y^2 -6x-6y+14=0 are two circles C_1, C_2 are the centre of circles and circles intersect at P,Q find the area of quadrilateral C_1 P C_2 Q (A) 12 (B) 6 (C) 8 (D) 4

if the distances from the origin to the centre of three circles x^2+y^2+2lambda_ix-c^2=0(i=1,2,3) are in G.P. ,then the lengths of the tangents drawn to them from any point on the circle x^2+y^2=c^2 are in

CENGAGE PUBLICATION-CIRCLE -Excercises (Single Correct Answer Type)
  1. Tangent are drawn to the circle x^2+y^2=1 at the points where it is me...

    Text Solution

    |

  2. If the line xcostheta=2 is the equation of a transverse common tangent...

    Text Solution

    |

  3. Let C1 and C2 are circles defined by x^2+y^2 -20x+64=0 and x^2+y^2+...

    Text Solution

    |

  4. The circles having radii r1a n dr2 intersect orthogonally. The length ...

    Text Solution

    |

  5. The two circles which pass through (0,a)a n d(0,-a) and touch the line...

    Text Solution

    |

  6. Locus of the centre of the circle which touches x^2+y^2 - 6x-6y+14 =0 ...

    Text Solution

    |

  7. If the chord of contact of tangents from a point P to a given circle p...

    Text Solution

    |

  8. If the angle of intersection of the circle x^2+y^2+x+y=0 and x^2+y^2+x...

    Text Solution

    |

  9. The coordinates of two points Pa n dQ are (x1,y1)a n d(x2,y2)a n dO is...

    Text Solution

    |

  10. If the circumference of the circle x^2 + y^2 + 8x + 8y - b = 0 is bise...

    Text Solution

    |

  11. Equation of the circle which cuts the circle x^2+y^2+2x+ 4y -4=0 and ...

    Text Solution

    |

  12. The minimum radius of the circle which contains the three circles, x^...

    Text Solution

    |

  13. about to only mathematics

    Text Solution

    |

  14. If a circle passes through the point (a, b) and cuts the circle x^2 + ...

    Text Solution

    |

  15. The centre of the smallest circle touching the circles x^2+ y^2-2y -3=...

    Text Solution

    |

  16. Two circle with radii r(1) and r(2) respectively touch each other exte...

    Text Solution

    |

  17. Consider points A(sqrt13,0) and B(2sqrt13,0) lying on x-axis. These po...

    Text Solution

    |

  18. The common chord of the circle x^2+y^2+6x+8y-7=0 and a circle passing ...

    Text Solution

    |

  19. If the circumference of the circle x^2+y^2+8x+8y-b=0 is bisected by th...

    Text Solution

    |

  20. The equation of the circle passing through the point of intersection o...

    Text Solution

    |