Home
Class 12
MATHS
Find the value of a if x^3-3x+a=0 has th...

Find the value of `a` if `x^3-3x+a=0` has three distinct real roots.

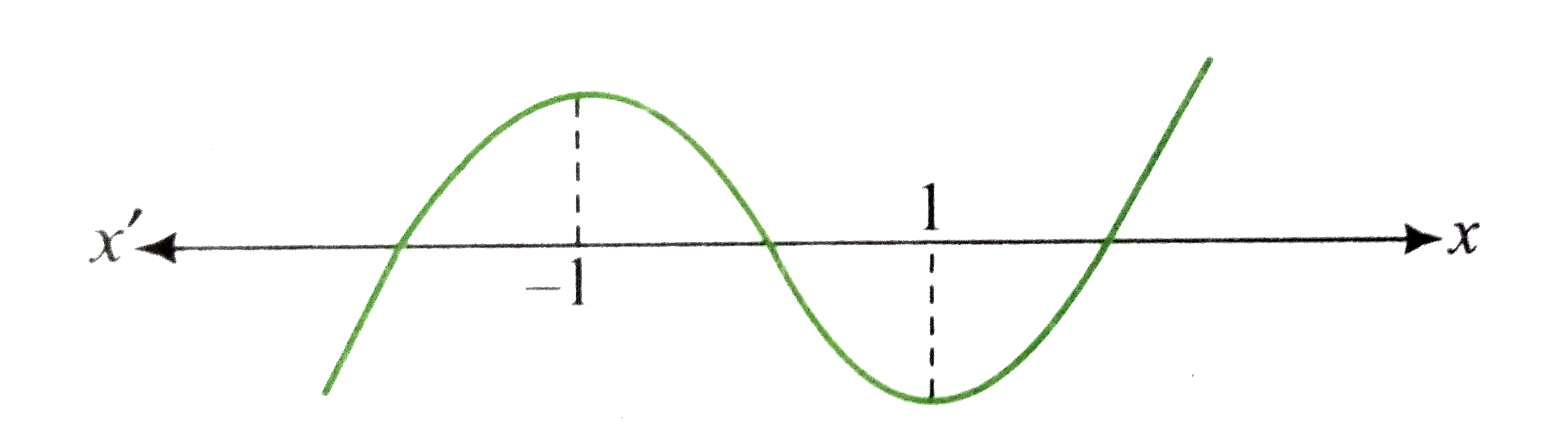
Text Solution

Verified by Experts

The correct Answer is:
`-2 lt a lt 2`
Let `f(x) = x^(3) - 3x = a`
Let `f'(x) = 0`
`rArr 3x^(2) - 3 = 0 or x = pm 1`

For three distinct roots , `f(1) lt 0 and f (-1) gt 0`
`rArr 1 -3 + a lt 0 and - 1 + 3 + a gt a`
or `a lt 2 and a gt - 2`
or ` - 2 lt a lt 2`
Promotional Banner

Topper's Solved these Questions

  • THEORY OF EQUATIONS

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 2.7|9 Videos

  • THEORY OF EQUATIONS

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 2.8|11 Videos

  • THEORY OF EQUATIONS

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 2.5|4 Videos

  • STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise ARCHIVES (NUMERICAL VALUE TYPE)|1 Videos

  • THREE DIMENSIONAL GEOMETRY

    CENGAGE PUBLICATION|Exercise All Questions|291 Videos

Similar Questions

Explore conceptually related problems

Find the value of k if x^3-12x+k=0 has three real distinct roots.

The real number k of for which the equation 2x^3+3x+k=0 has two distinct real roots in [0,1]

The real number k for which the equation 2x^(3)+3x+k=0 has two distinct real roots in [0, 1]

The number of values of k for which the equation x^3-3x+k=0 has two distinct roots lying in the interval (0,1) is (a) three (b) two (c) infinitely many (d) zero

Without solving, find the values of 'p' for which the equation x^2 + (p -3)x +p = 0 has real and equal roots.

Number of integral values of b for which the equation (x^3)/3-x=b has three distinct solutions is____

Consider an unknown polynomial which when divided by (x-3) and (x-4) leaves 2 and 1 as remainders, respectively, Let R(x) be the remainder when the polynomial is divided by (x-3) (x-4). If the equation R(x)= x^2+ax+1 has two distinct real roots then values of 'a' are-

If a continuous function f defined on the real line R assume positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative, then the equation f(x)=0 has a root in R. Consider f(x)= ke^(x)-x , for all real x where k is a real constant. For k > 0, the set of all values of k for which y=ke^(x)-x=0 has two distinct roots is

If x^2+(a-b)x+(1-a-b)=0. where a ,b in R , then find the values of a for which equation has unequal real roots for all values of bdot