A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TRIANGLES
S CHAND IIT JEE FOUNDATION|Exercise Question Bank|30 VideosTRIANGLES
S CHAND IIT JEE FOUNDATION|Exercise Self Assessment Sheet|10 VideosTIME AND WORK
S CHAND IIT JEE FOUNDATION|Exercise Self Assessment Sheet - 20|10 VideosTRIGONOMETRICAL RATIOS
S CHAND IIT JEE FOUNDATION|Exercise Self Assessment Sheet - 40|1 Videos
Similar Questions
Explore conceptually related problems
S CHAND IIT JEE FOUNDATION-TRIANGLES -Self Assessment Sheet
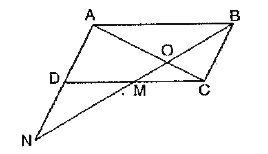
- In the given figure, M is the mid-point of the side CD of the parallel...
Text Solution
|
- In right triangle ABC, right angle at C, M is the mid-point of the hyd...
Text Solution
|
- AD is angular bisector of AABC such that BD:DC = 2:3. If AB = 7cm, wha...
Text Solution
|
- In the given figure DE || BC. AD=x, DB=x-2 AE=x+2, EC=x-1 W...
Text Solution
|
- If in Deltas ABC and DEF, angleA=angleE=37^(@), AE : ED = AC : EF and ...
Text Solution
|
- Triangles ABC and DEF are similar. If the length of the perpendicular ...
Text Solution
|
- In the given figure, ABCD is a parallelogram. E and F are the centroid...
Text Solution
|
- In a DeltaABC, perpendicular AD from A on BC meets BC at D. If BD = 8 ...
Text Solution
|
- If E is a point on side r:A of an equilateral triangle ABC such that B...
Text Solution
|
- In a right triangle ABC right angled at C, P and Q are points on the s...
Text Solution
|
- In figure, ABC is a right triangle, right angled at B. AD and CE are t...
Text Solution
|